\n", "\n", "\n", "*Edit: a reader pointed out that the original creator of this animation [posted it on reddit](https://www.reddit.com/r/mathpics/comments/4nd5h1/41_triple_pendulums_with_very_slightly_different/) in 2016.*\n", "\n", "Naturally, I immediately wondered whether I could reproduce this simlulation in Python.\n", "This post is the result.\n", "\n", "" ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "This should have been pretty easy. After all, a while back I wrote a [Matplotlib Animation Tutorial](https://leeblog.org/blog/2012/08/18/matplotlib-animation-tutorial/) containing a double pendulum example, simulated in Python using SciPy's [``odeint`` solver](https://docs.scipy.org/doc/scipy-0.17.0/reference/generated/scipy.integrate.odeint.html) and animated using matplotlib's [animation module](http://matplotlib.org/api/animation_api.html).\n", "All we need to do is to extend that to a three-segment pendulum, and we're good to go, right?" ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "Unfortunately, things are not so simple.\n", "While the double pendulum equations of motion can be solved [relatively straightforwardly](http://scienceworld.wolfram.com/physics/DoublePendulum.html), the equations for a triple pendulum are much more involved.\n", "For example, the appendix of [this document](https://www.nickeyre.com/images/triplependulum.pdf) lists the three coupled second-order differential equations that govern the motion of the a triple pendulum;\n", "here's a screenshot of just the first of those three:" ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "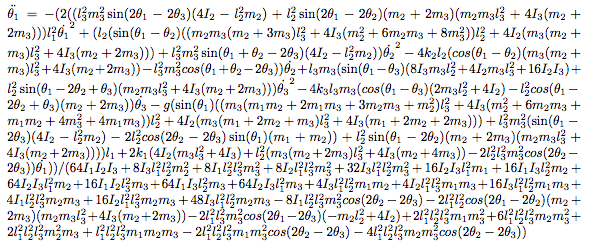" ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "Yikes." ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "Fortunately, there are easier approaches than brute-force algebra, that rely on higher abstractions: one such approach is known as [Kane's Method](http://docs.sympy.org/dev/modules/physics/mechanics/kane.html).\n", "This method still involves a significant amount of book-keeping for any but the most trivial problems, but the [Sympy package](http://sympy.org) has a nice implementation that handles the details for you.\n", "This is the approach I took to simulate the triple pendulum, borrowing heavily from [Gede et al. 2013](https://www.researchgate.net/publication/267490975_Constrained_Multibody_Dynamics_With_Python_From_Symbolic_Equation_Generation_to_Publication) who present a nice example of Sympy's API for applying Kane's Method." ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "## The Code\n", "\n", "The following function defines and solves the equations of motion for a system of *n* pendulums, with arbitrary masses and lengths.\n", "It's a bit long, but hopefully commented well enough that you can follow along." ] }, { "cell_type": "code", "execution_count": 1, "metadata": { "collapsed": false, "deletable": true, "editable": true }, "outputs": [], "source": [ "%matplotlib inline\n", "import matplotlib.pyplot as plt\n", "import numpy as np\n", "\n", "from sympy import symbols\n", "from sympy.physics import mechanics\n", "\n", "from sympy import Dummy, lambdify\n", "from scipy.integrate import odeint\n", "\n", "\n", "def integrate_pendulum(n, times,\n", " initial_positions=135,\n", " initial_velocities=0,\n", " lengths=None, masses=1):\n", " \"\"\"Integrate a multi-pendulum with `n` sections\"\"\"\n", " #-------------------------------------------------\n", " # Step 1: construct the pendulum model\n", " \n", " # Generalized coordinates and velocities\n", " # (in this case, angular positions & velocities of each mass) \n", " q = mechanics.dynamicsymbols('q:{0}'.format(n))\n", " u = mechanics.dynamicsymbols('u:{0}'.format(n))\n", "\n", " # mass and length\n", " m = symbols('m:{0}'.format(n))\n", " l = symbols('l:{0}'.format(n))\n", "\n", " # gravity and time symbols\n", " g, t = symbols('g,t')\n", " \n", " #--------------------------------------------------\n", " # Step 2: build the model using Kane's Method\n", "\n", " # Create pivot point reference frame\n", " A = mechanics.ReferenceFrame('A')\n", " P = mechanics.Point('P')\n", " P.set_vel(A, 0)\n", "\n", " # lists to hold particles, forces, and kinetic ODEs\n", " # for each pendulum in the chain\n", " particles = []\n", " forces = []\n", " kinetic_odes = []\n", "\n", " for i in range(n):\n", " # Create a reference frame following the i^th mass\n", " Ai = A.orientnew('A' + str(i), 'Axis', [q[i], A.z])\n", " Ai.set_ang_vel(A, u[i] * A.z)\n", "\n", " # Create a point in this reference frame\n", " Pi = P.locatenew('P' + str(i), l[i] * Ai.x)\n", " Pi.v2pt_theory(P, A, Ai)\n", "\n", " # Create a new particle of mass m[i] at this point\n", " Pai = mechanics.Particle('Pa' + str(i), Pi, m[i])\n", " particles.append(Pai)\n", "\n", " # Set forces & compute kinematic ODE\n", " forces.append((Pi, m[i] * g * A.x))\n", " kinetic_odes.append(q[i].diff(t) - u[i])\n", "\n", " P = Pi\n", "\n", " # Generate equations of motion\n", " KM = mechanics.KanesMethod(A, q_ind=q, u_ind=u,\n", " kd_eqs=kinetic_odes)\n", " fr, fr_star = KM.kanes_equations(forces, particles)\n", " \n", " #-----------------------------------------------------\n", " # Step 3: numerically evaluate equations and integrate\n", "\n", " # initial positions and velocities – assumed to be given in degrees\n", " y0 = np.deg2rad(np.concatenate([np.broadcast_to(initial_positions, n),\n", " np.broadcast_to(initial_velocities, n)]))\n", " \n", " # lengths and masses\n", " if lengths is None:\n", " lengths = np.ones(n) / n\n", " lengths = np.broadcast_to(lengths, n)\n", " masses = np.broadcast_to(masses, n)\n", "\n", " # Fixed parameters: gravitational constant, lengths, and masses\n", " parameters = [g] + list(l) + list(m)\n", " parameter_vals = [9.81] + list(lengths) + list(masses)\n", "\n", " # define symbols for unknown parameters\n", " unknowns = [Dummy() for i in q + u]\n", " unknown_dict = dict(zip(q + u, unknowns))\n", " kds = KM.kindiffdict()\n", "\n", " # substitute unknown symbols for qdot terms\n", " mm_sym = KM.mass_matrix_full.subs(kds).subs(unknown_dict)\n", " fo_sym = KM.forcing_full.subs(kds).subs(unknown_dict)\n", "\n", " # create functions for numerical calculation \n", " mm_func = lambdify(unknowns + parameters, mm_sym)\n", " fo_func = lambdify(unknowns + parameters, fo_sym)\n", "\n", " # function which computes the derivatives of parameters\n", " def gradient(y, t, args):\n", " vals = np.concatenate((y, args))\n", " sol = np.linalg.solve(mm_func(*vals), fo_func(*vals))\n", " return np.array(sol).T[0]\n", "\n", " # ODE integration\n", " return odeint(gradient, y0, times, args=(parameter_vals,))" ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "## Extracting Positions\n", "\n", "The function above returns generalized coordinates, which in this case are the angular position and velocity of each pendulum segment, relative to vertical.\n", "To visualize the pendulum, we need a quick utility to extract *x* and *y* coordinates from these angular coordinates:" ] }, { "cell_type": "code", "execution_count": 2, "metadata": { "collapsed": false, "deletable": true, "editable": true }, "outputs": [], "source": [ "def get_xy_coords(p, lengths=None):\n", " \"\"\"Get (x, y) coordinates from generalized coordinates p\"\"\"\n", " p = np.atleast_2d(p)\n", " n = p.shape[1] // 2\n", " if lengths is None:\n", " lengths = np.ones(n) / n\n", " zeros = np.zeros(p.shape[0])[:, None]\n", " x = np.hstack([zeros, lengths * np.sin(p[:, :n])])\n", " y = np.hstack([zeros, -lengths * np.cos(p[:, :n])])\n", " return np.cumsum(x, 1), np.cumsum(y, 1)" ] }, { "cell_type": "markdown", "metadata": { "deletable": true, "editable": true }, "source": [ "Finally, we can call this function to simulate a pendulum at a set of times *t*.\n", "Here are the paths of a double pendulum over time:" ] }, { "cell_type": "code", "execution_count": 3, "metadata": { "collapsed": false, "deletable": true, "editable": true }, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYYAAAD8CAYAAABzTgP2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl8TFf7wL93JpM9shPZhCSIJQli3/ed0lZVtVp9qxSl\nSrVVmtpfaquq0io/aqvS2pfYl9gSOxEishLZ922Sub8/RkZC9kwSvPfrMx93zj333OdmZu5zz3Oe\nRRBFEQkJCQkJiTxk1S2AhISEhMTLhaQYJCQkJCQKICkGCQkJCYkCSIpBQkJCQqIAkmKQkJCQkCiA\npBgkJCQkJAogKQYJCQkJiQJIikFCQkJCogCSYpCQkJCQKIBOdQtQHqysrEQnJ6fqFkNCQkLilcLf\n3z9WFEXrkvq9korByckJPz+/6hZDQkJC4pVCEITQ0vTTiilJEIQ+giAECoIQJAjC14XsnyYIwrWn\nr1uCIOQKgmDxdF+IIAg3n+6T7vYSEhIS1UyFZwyCIMiBVUBPIAK4LAjCHlEU7+T1EUVxMbD4af+B\nwBeiKMbnG6arKIqxFZVFQkJCQqLiaGPG0AoIEkUxWBTFbGAbMLiY/u8CW7VwXgkJCQmJSkAbisEO\nCM/3PuJp2wsIgmAI9AF25msWgaOCIPgLgjCmqJMIgjBGEAQ/QRD8YmJitCC2hISEhERhVLW76kDg\n3HNmpA6iKHoCfYHxgiB0KuxAURTXiqLoJYqil7V1iYvqEhISEhLlRBuKIRJwyPfe/mlbYQznOTOS\nKIqRT/+PBv5BbZqSkJCQkKgmtKEYLgOugiDUFQRBF/XNf8/znQRBMAU6A7vztRkJgmCStw30Am5p\nQSYJCQkJiXJSYcUgimIOMAE4DAQAf4mieFsQhLGCIIzN13UIcEQUxbR8bbWAs4IgXAcuAftFUTxU\nUZkkJCQkSkNwUjArr64kR5VT3aK8VGglwE0UxQPAgefafn3u/QZgw3NtwYCHNmSQkJCQKCvHQo+x\n9sZabsTcYFGnRZjrm1e3SC8FUq4kCQmJ/1k+cf+E2e1m4//En+H7hnMn7k7JB/0PICkGCQmJ/2mG\nuA5hY9+N5Iq5jDo4iuNhx6tbpGpHUgwSEhL/8zSxasL2AdtxNXfli5NfsP3u9uoWqVqRFEM14hvp\nS1BCUHWLISEhAVgaWPJ7r9/paNeRuRfnsu7muuoWqdqQFEM1kZCZwKdHP2WW76zqFkVCQuIphgpD\nlnddTr+6/Vh+Zfn/rHJ4JdNuvw5ciroEgL6OfjVLIiEhkR8dmQ7zOswDYPmV5QiCwOgmo6tZqqpF\nUgzVxNa76gDwYfWHVbMkEhISz5OnHERRZJn/Miz1LRnsUlxu0NcLSTFUE/5P/AHo6ti1miWRkJAo\njDzlkJCVgLevN9aG1rSzbVfdYlUJ0hpDNZCZk6nZ1pXpVqMkEhISxaGQK1jWZRn1zOox9eRUwlPC\nSz7oNUBSDNXAmcgzmm1BEKpREgkJiZIw1jVmRdcVCILAlJNTCjzYva5IiqEaOPTwWTqoXFVuNUoi\nISFRGuxN7FnQcQF34++y4NKC6han0pEUQxWTrkzndMRpzfuMnIxqlEZCQqK0dLLvxMdNPmbX/V0F\nfsOvI9LicxVzKuIUmbmZ9K/Xn/3B+0lTpmGsa1zdYkm8pIiiSEJWAlFpUaQp1YmJjRXG1DaqjZm+\nWTVL9/ogiiIxGTFEpEQQmRpJXEYcGTkZPEh6wLXoayRmJWKqa4pHTXXOz5nnZrLnjT2Y6plWs+SV\ng6QYqphDDw9hbWBNe9v2asWQk1byQUB4SjgXHl8gKSuJBuYNaG/XHpkgTfheR+Iz4zkaepRTEae4\nGXOThKyEQvvVNKyJVy0vujp2patDV/TkelUs6auLMlfJ1eirXIy6yO3Y29yOu01iVmKxx0RnROMT\n6gOoP6MO2zowp/0cBjsPfu3WCiXFUIWkZqdyNvIsbzd4Gwt9CwCSspKKPSYqLYqlfks5FHIIEVHT\n3sepD/M7zkchU1SqzBJVgyiKnIk8w+aAzVx8fJFcMRdHE0c6O3Smvnl9bI1tMVGYAJCUnURkSiR3\n4u9w4fEFDjw8gKmeKSMajuD9Ru9jomtSzVfzcpKSncLxsOP4hPpwKeoSGTkZyAU5zmbOdHPsRkOL\nhjiYOBCZEsnci3Mx0DHgw8Yf0qNOD+yN7UnISuBc5Dn+uf8Pt+LU9cRmnpvJzHMzmdV2Fm+5vvXa\nKAhJMVQhJ8JPkK3Kpo9THwx0DACISY8psv/BhweZc34OOWIOo5uMZojrEKwNrNkcsJmfrv5EQ4uG\nfNz046oSX6ISEEWRE+En+PX6rwTEB1DbqDajm4ymt1Nv6pvXL/FGk6vK5VLUJbbc3cLq66vZHrid\naS2n0b9u/9fmJlURclW5nI08y677uzgTeQalSomtkS2DnAfR3rY9LW1aFjDlXo2+ysLLC3Exc2F1\nj9XYGNlo9hkqDBnWYBjDGgwjTZlGmy1tNPtmn5/N7POzOfrWUWoZ1arSa6wMJMVQhRwKOYSNkQ3u\n1u4kZKrNA7EZsS/0E0WRVddWsebGGjysPVjQYQEONZ6V1f7E/RNuxN7gt5u/MbzhcIwURlV2DRLa\nIyw5jB/O/8ClqEs4mDgwu91sBjgPKNMsUC6T09a2LW1t23I77jbzL8znmzPfcDriNN5tvTFUGFbi\nFby8xGfG81fgX+y8v5OotCgs9S15p8E79K3bl6ZWTQtVmvGZ8Uw9NZXaRrXZ0GdDsesHRgojvm/7\nPT+c/4FxHuNYfX01AD3+7sGWfltoat200q6tKpCM1FVEUlYSvo986V2nNzJBhrm+OXJB/oJiUIkq\nvvf9njU31jDEZQjr+6wvoBTyGN1kNGnKNCl3/CtIjiqHP279wdA9Q7kTd4fvWn/Hnjf2MMR1SIVM\ng40tG7Ox70YmNpvI4ZDDfHjow2JnpK8j4SnhzLswj95/92bVtVXUrVGXpV2W4vO2D9NbTcfd2r3I\nmdQSvyUkZCawpPOSUi0qD3EZgqu5K/uD9+M30o8Odh0AGHFgBNdjrmv1uqoaSTFUEacjTpOjyqG3\nU28AZIIMS33LAopBJarw9vXmn6B/GOsxlh/a/VDkjcLT2pPaRrU5Gnq0SuSX0A5xGXGM8RnDMv9l\ntLdtz7+D/+Wdhu+gI9PO5F0ukzPGfQwru60kJDmE0YdHE50erZWxX2YepT5i1rlZDPxnIH/f/5u+\ndfuye/Bu1vZaS886PUtUuLfjbrPnwR7eb/Q+bpZupTqnXCZnrPtYwlLCOBV+itU9VvN5s88BGHlg\nJA+THlb4uqoLSTFUEWcizmCpb0ljq8aaNitDK6Iz1D9aURRZeGmhRimM9xxfrI1YEARa126Nf7Q/\nKlFV6fJLVJzrMdcZtm8YN2JuMK/DPFZ0W1Fp9uhO9p34tcevRKdHM+7oOFKzUyvlPNVNfGY8Cy8t\nZMA/A9gXvI93G77LoaGHmN1+NvXM6pV6nJVXV2KuZ85/mv6nTOfv7tidOjXqsO7WOkRR5BP3Txjj\nPgaAQf8OemXjlLSiGARB6CMIQqAgCEGCIHxdyP4ugiAkCYJw7elrVmmPfR3IUeVw7tE5Oth1KOBi\namtkS1RqFAAb72xk692tjGo0is88PivVuF61vEjKSiI4MbhS5JbQHnsf7OXDQx+ikCn4s9+fDHIe\nVOnnbF6rOcu6LCM4MZhvzn7zWj1AKHOVbLy9kQG7BrDt7jYGOQ/iwNADTG81vczK9n7Cfc5FnmNk\no5Fl9uiSy+SMajyKO3F3uBh1EYCJzSZS37w+AL3+7oUoisUN8VJSYcUgCIIcWAX0BRoB7wqC0KiQ\nrmdEUfR8+ppdxmNfaW7G3iQ5O5mO9h0LtNsa2/Io7RE+oT4s8VtCzzo9meI1pdTeJHlT3rsJd7Uu\ns4T22BywmW/PfkuLmi3YPmA7DS0aVtm529m1Y2rLqZwMP8mmO5uq7LyVyflH5xm6ZyiL/Rbjbu3O\nrkG78G7nXcCDqCz8GfAn+nJ93q7/drmOH+Q8CCsDKzbe3qhp29xvMwCJWYn8GfBnucatTrRh2GwF\nBImiGAwgCMI2YDBwp5KPfWU4E3EGuaD2HsmPrbEtGTkZTDk5BXdrd+Z3mF+moLW6pnVRyBQExgcy\noN4AbYstkUdONsTeg7j7EB8MccGQ8BDS4yEnA5QZoMxUb+dmg44+GFggGlrwq6GMX0iku74ti8xa\novvoBtR0A0NLqCJ30hENR3Dx8UV+uvITHe07Us+09CaWl4n4zHgWX17MvuB9OJo4sqr7KjradayQ\nW25GTgYHHx6kX71+mOubl2sMPbkeQ1yGsO7WOqLTo6lpWBN9HX0mN5/M8ivLWXR5Ee3t2r9Sf3dt\nKAY7IH8u2gigdSH92gmCcAOIBKaKoni7DMciCMIYYAyAo6OjFsSuOs5EnsGzpic1dGsUaDfTe5bS\nYFmXZWWu5qaQKXAxcyEwPlArcv5PkxgOAXvg7n4IPVexsXIyIeURy3XS+MPQlMEpqXg/vIBOwIWS\nj/1gNzh1BJm8YjLkQxAEZrWdxeB/BzP/wnx+6/XbKxXjIIoi+x/uZ+GlhaQp0xjjPoYx7mO0Eul9\nOuI0GTkZ9Kvbr0LjDHIexG83f2Nf8D5Ntbe36r/F8ivLAfjB9wc29NnwyvzdqyqO4QrgKIpiqiAI\n/YB/AdeyDCCK4lpgLYCXl9crY7RLyEzgbvxdJjabWKBdFEXW3lgLwDsN3qGmYc1yjV/fvH6BNN4S\npSBgL2wfWbZjrBqAlStY1ANLZzCvC0ZW6tmBwhAU+qBjAHJdyMnkjxtr+OP2Hwyzac8Mz67IkiMg\nIRRiAiG8GAWx8bkqYbbNodUYaDIUdMp/I7QysGK853gWXFrAyfCTr0yBqPjMeOacn8PRsKN4WHvw\nQ7sfcDZz1tr4hx4ewlLfEq9aXhUax8nUiWY1m7E7aDcfNf4IQRAw1TOlTe02XHh8gSvRVzgSekTj\nlfiyow3FEAnkd7S3f9qmQRTF5HzbBwRB+EUQBKvSHPuqc+XJFQBa2rQs0L77wW6Ck9SLxrbGtuUe\n39Xcld0PdhOfGY+FvgU5qhyCEoMITQ4lNiOWzJxM5IIcI10jbAxtqGdWD1sj21fmyUUrXP4d9n9Z\nfB8Dc3AbpH45tQeFQblPtzPkIMtu/0Ffp77M6LSwZPOgKELQMbj2JymJoYTF3CJMoUO0XE5cRjCx\nZ2cQf34maTIZmTI5GUYWZCr0AQFBEJAhQybIMFAYYKwwxlBhiLHCGEt9S6wNrbEysMLawJrWtVtj\nZ2zHL9d/oYtDl5f+O3Ay/CTf+35PSnYKU1pM4YNGHyDX4kwqNTuVM5FneNP1Ta2MO9h5MN7nvbkZ\nexN3a3dA7R124fEFaujWYNW1VfRw7KHVa6gstKEYLgOugiDURX1THw6MyN9BEAQb4IkoiqIgCK1Q\nL3rHAYklHfuq4/fED325Pk0sm2jaIlIiWHhpIS1qteBe/D0epT4q9/iuZuqJ17RT0xARuRV7q0QX\nOQt9Czrbd6a7Y3fa2LZ5/ZKvZSTCf+sU30dhBGNOgnV9rZ76WOgxZl+YTXu79szrMK9IpaASVYQk\nhXA77jYB8QEExAXwIDeYBN0EsHu2iKor6GApgkVWGsYqETNlNgYJj9ETRQRABYiObcg1r0OGMoM0\nZRpJmUlEpEQQlxFHqrJwN1X3je580OgDGlo0pIFFA8161ctAVm4WS/2WsuXuFhpaNOT3Xr/jal4m\nA0OpOBF+gqzcLPrW7auV8Xo79WbexXkcCTmiUQx5/3e078j+4P0cDTv6SswaKqwYRFHMEQRhAnAY\nkAN/iKJ4WxCEsU/3/wq8BYwTBCEHyACGi2ofrkKPrahMLxOXoy7jUdMDhVz9o8tV5TLj7AwA5neY\nz+QTk4lMLfskSZmrZG/wXo056lLUJRpbNmaIyxA8rD1wNnPG2tAafbk+IiIp2Sk8TnvM/YT7+D3x\nwyfUh3+C/sFEYcKwBsMY2WgkVgZW2rvwqiY1Bn50KXq/U0cYubNC5piSCIwP5Juz39DEsglLOy/V\nfOZ5hCWH4fvIl0tRl/CL8tNkTdWX61Pfoj7d63SnjkkdHGo44GjiiI2RDcYK44JP9jH34NRCuLXz\nWVvsgWfbfRdB6081bzNyMohNjyU6I5qIlAgeJD1g/a31AGwP3E5WbhagXq9qYN6AZrWa0aym+lUd\n34eHSQ+ZdmoagQmBvN/ofSY3n4yuvHLK3+ZPUaMNjHWNaWXTilMRp5jaciqgNvXKBBl2xnbYG9uz\n9e7WV0IxCK+ij62Xl5fo5+dX3WKUSGp2Ku22tmOcxzjGeY4D1K6LCy8tZG77uQx2GcwXJ74gOCmY\n3W/sLtWYSpWS3UG7WXtjLY/THuNs6syDpAd0tu/Mz91/LrVsylwll6Iusev+Lo6GHUVH0GGI6xDG\ne44vt3dGlSOK8HNLtbdQYXx6Gmp7VIkoiZmJDN8/HGWukm0DtmFtaI0oigTEB3A09Cgnwk8QlBgE\nQC3DWrSyaUVLm5Y0tWqKk6lT+SKfVSrY/h4EHih8fxHX/8u1X1h9fTUHhx4kKzeLu/F3uRt/l5ux\nN7kVe0ujLOrUqEOb2m1ob9ueVrVbVXpOriMhR5h5biZ6cj3mdphLJ/tOlXaupKwkumzvwshGI/nS\nqwQzYxnYErCFBZcWsG/IPurUUM9ae//dmxa1WuBs5szyK8vZ/cbuavNQEgTBXxTFEhdUpCR6lcid\nuDuIiJonkqi0KH668hPt7dprApzsjO04G3kWURRLtPn6Rvoy58IcIlIjaGrVlFltZ9Hetj0fHvqQ\nlOyUMsmmkCtob9ee9nbtCUsOY/3t9ey8t5NDIYeY1HwSb7q++fLWewj1hfVFTP+n3IUatatUnBxV\nDtNOTyM6PVrjefJ/t/+Pf4P+JSgxCJkgo0WtFkxvOZ1O9p1wMHHQjn1fJoN3tz57v+8L8Pvj2fs1\nT2+sdl7wyTFN84B6A1h9fTU+oT581OQjnM2c6V+vP6B+YLgTf4erT65y+cll9jzYw/bA7egIOnjW\n9KSLQxd61OmBnbFdxeV/ilKlZLn/cjbe2YiHtQdLOi+p9AylR0OPkiPm0KduH62O28m+EwsuLeBU\n+Ck+aPwBADZGNjxOe8wUrymsuLKCQw8P8Zln6YJYqwtJMVQiN2NvAurkZqIoMu/iPEREvmv9nebG\nYGtsS2ZuJnGZcUVO3RMzE1l0eRF7g/fiVMPpBf9tZzNnDoccLpVyKQzHGo583/Z73mv4HvMuzmP2\n+dn8G/QvCzssLDSBX7WxdxL4b3ix/eOj4NDyxfYqYuXVlVx4fIF3G77L5oDNHAk5Qo6Yg7u1OzPb\nzKRnnZ5VMwsbsEz9UqlgWSNIeaxuj/QD76dJ4aaH4ljDkcaWjTWKIT8KuQIPaw88rD34sMmHZOdm\ncy36GuceneNs5Fl+9PuRH/1+xM3CjR51etDbqbfmybg8JGQmMOXkFPye+DGi4Qimek19wQRXGRwK\nOYSjiSONLLQbT2tvYo+LmQunI05rFIO1oTWB8YFYGVjRolYLfEJ9JMXwv8ztuNs4mDhgpm/G0dCj\nnAw/yZctvsTexF7TJ+/J61Hqo0IVw9nIs8w4O4PkrOQi/bddzFzYkb2DmIyYcru9AriYu/BH7z/Y\nF7yPBZcW8Pa+t/Fu6631p6oys9wdEkMLtj33FFxdXI66zB+31E/pW+9uxUhhxPCGw3m7/ttlytWj\nVWQy+PJpNPzzs6uni/Kde3/F6nvbSchMKFZp6cp1aVW7Fa1qt+KLFl8QnhzOsbBj+IT5sPLqSlZe\nXYmHtQeDnAfR26l3mUpdBicFM+HYBJ6kPWF+h/kMdB5YrsstK7EZsVyKusR/mv6nUjyzOtp3ZNPt\nTaQr0zFUGGKoY0h6TjoA3Ry7sejyIh6lPqqQN2Jl85LaCl4PbsbepIlVEzJzMll8eTENzBswslFB\n//m8L8fznkkqUcXqa6v57OhnWBpYsm3ANiY2m1ioB1Gex0ZQQlCFZRYEgYHOA/l74N+4mLkw7fQ0\nvH29NXbnKmWxq/pJN79SeHMdeCe9FErh0uNLjD6sDmYy0TXhyxZf4vOWOr1ztSmF56nTTv33mvGk\nQHP7k8sREbkUtK9MwznUcODDJh+yud9mfN7yYUqLKaQp05hzYQ5d/+rKlye/5OLjiyXmB7rw+AIj\nD4wkTZnGut7rqkwpAPiE+qASVfR10o430vN41fIiR8zhdpzaj8ZQYUiGUu0p2Ka2urjPxccXK+Xc\n2kKaMVQSSVlJRKVF4WbhxqY7m3iU9og/OvzxwiJjnmLI75mUlJXE9DPTORd5jkHOg/iuzXeaim+F\nkRfwE5QYRDu7dlqR39bYlvV91rPq6irW3VrHg8QHLO+6HEsDS62MXyw/1ofUgjcyxp4Fm5ej+Eli\nZiLLrixj1/1dgLrM6twOc19ut1+FvlpBiCLMt8UtKx1dlciN49/R++8J8E0k6BmXPE4+bIxs+KjJ\nR3zY+EMC4gPY+2Ave4P3ciT0CHVN6/JOg3cY5DzohcR0O+7tYN6FedQ1rcvP3X/W6npFaTj08BAu\nZi64mBfjxVYBPKzVC/7Xoq/R0qYlOoIOOWIOoJ7dW+hb4PfEjyGuQyrl/NpAUgyVRJ4HipmeGQsv\nLaS7Y/cXgtxAXQnKTM9Moxii0qL41OdTwlPCS11H1kLfAgt9C805tYVCpmByi8m4Wbox4+wM3jvw\nHqu6r9Jq5GkBTsyHU/8t2PbZRahZdUnnikMURfYG7+XHyz9qXE1HNRqlcU18JRAEmPEYhSjitrYh\nt/SeuoIueHpz9i6+BnnhQwo0smxEI8tGTGo+icMhh9l2dxsLLy1kxZUVDHEZwqjGo6hlWIsl/kvY\ndGcTHew6sLjT4gJlNauCqLQorkRfYYLnhEo7h6meKfVM63Et5hoAuWIuckEd1CYIAo0tG3Mn7uVO\nBycphkoiz6xz8OFBslXZTGkxpci+dsZ2RKZGEpQQxKdHPyVDmcHanmvxsil9mL6rmSv3E4pw26wg\nvZ16Y2tky8TjExl5YCTLuy6nde1CU1qVj4wE+K9Twbbn/PGrm6SsJLx9vTkadhRnU2cSshJoYtmE\nyS0mV7do5UMQcHUfoS709DhfIR9vU+j8NXT9plzD6uvoM9hlMINdBnMr9hZb727lr8C/2HJ3i6bP\ne27vMdVrqtaKE5WFwyGHASp93cyzpifHwo6hElXkirkFPPwaWzXm3KNzZORkFGsJqE6kNYZKIu/p\n/cLjC7zX8D0caxSd+M/exB7fR758cOgDVKKK9X3Wl0kpADS0aMi9hHsoc5UVkrsomlo3ZWv/rdgY\n2TDu6DiOhWnJxu9tWlAp6NVQP7W+RErhWvQ13tr7FifDTzKlxRRa1W6FgMB3bb+rlpubtnCq4URi\nViKJX4fCpBvPdpxaqP5cMpOLPrgUNLFqwrwO89g2YFuB9siUyEp7iCmJQw8P0ciyUYU8qUqDp7Un\nSVlJhCSFvKAAXM1cUYkqQpNDixmhepEUQyWRpxgMFYYlVoVKzEwEoIZuDTb13UQDiwZlPl8TqyZk\nq7K5n1h5P7jaxuoi6W6Wbkw5OYV/7v9T/sESw565UOYxKwG+CS+8fzWx58EePjr8ETqCDpv6baKd\nbTu2B25nWINhNLZsXPIALzF5tv2o9Cgwr6NWyL3mPuuw0AF2flKhczxJe8LXZ75GIVPg3dab8Z7j\nuRJ9hWH7hjHl5JQqLTIVnhzOrbhblbbonJ+82KVbcbdIyU4psM6Sp5QkxfA/iN8TdWT2SLeRmOmb\nFdkvIC5AU/lpfof5BVxZy0JeydBbsbfKdXxpMdUz5beev9HapjWzfGeVr/jLYldYnm8hud+P6puS\n7OX5OoqiyM9Xf2bG2Rk0r9mcbQO20ciyEfMuzsNU1/SFbLmvInmOBHEZcc8a202E7xOfvb/5l1qB\nl2MmGpocygcHP+BR6iNW91jNm/XfZKzHWA6+eZCxHmM5F3mOIXuG8O2ZbyuUL6y0HAo5BFAlKSkc\naziiI9PhQeIDUrJTCqTcdzBRxwaFJYdVuhzl5eX5Jb5GZOZkarbzglwKIyghiE99nplMKuISam9s\nj5memcZFrjIxVBjyc/ef6VmnJ4suL9L48ZeIKKpvMmn5bdpJ0KpiT6XaRhRFFl1exJobaxjiMoRf\ne/yKqZ4pBx8e5Gr0Vb5o8UWZ/PVfVvKuIW8hXYMgqD+XIWuetc2xgiulfwgIiAvgg4MfkJGTwR99\n/iiwJlVDtwbjPcdz6M1DjGo0iiOhRxj07yBWXl1JujK9QtdUFKIocuDhATytPaltXPmR8QqZAqca\nTjxIfEBsRmwBbz5DhSEmuiZEp0cXM0L1IimGSsAn1AdQV1h7vjhPHo9THzPGZww6Mh3W9VoHQHhK\n+c0ogiDQxKoJ16Ovl3uMsqAr12VRp0X0derLMv9l/H7z9+IPiLoJP+SbOTUbWS4PmMomTyn8GfAn\nI91G8kO7H1DIFShzlfx89WcamDdgsMvgkgd6BdCXqwtDFbku5TFcbd7LY8+EF81/hXA56jIfHf4I\nPbkeG/tuLNLkZq5vzhSvKewbso/ujt1Ze2MtA/8ZyJ4He7Ren/pu/F2CEoOqNF7CxcyFoMQgotOj\nsTawLrDP2sCa2IzYKpOlrEiKoRKYc2EOAF+1/KrQ/WnKNMYfH09GTgZreq7By8YLhUxBREpEhc7b\nolYLHiQ9ICEzoeTOWkBHpsP8jvPpV7cfK66sYM31NYV33D0efu3w7P3XYTB4VZXIWFbW3FijUQpf\ntfxK4yq86/4uIlIjmNR80subQ6qM5GUtzc7NLrqTTPaiAi9GOZwKP8VYn7HYGNqwse9GnEydSpTD\nxsiG/3b6L5v6bqKmYU1mnJ3B+wff517CvdJcRqnYG7wXhUxRpZlNnc2ciUyNJFWZirVhQcVgZWBF\nXGZcEUdWP6/HN/wlIiw5TFMPob75i7n+c1W5fHX6K4ITg1nSeQmu5q6atLwVmTGAWjEAXIm+UqFx\nyoKOTEedzqDeQH6+9jOrr60u2MHbFK7mK4bunQT6L6cZ5nDIYVZdW8XAegMLKAVlrpLfb/2Op7Un\nHew6lDDrC1IxAAAgAElEQVTKq0OOSh10VSrPKu8k6JTvQcfbFLILmn2Ohx1n8snJuJq7sqHPBmyM\nbCgLnjU92dx/M3PbzyU8OZx39r7DiisrCphmy0OOKocDwQfoZN+pSk2A+eN9ng/iM9E1KbJWxsuA\npBi0zP/d/j/NdmG5j370+5HTEaf5tvW3BaKUHUwcKqwYGls2Rk+uh/8T/wqNU1bkMjlz2s9hsPNg\nfrn+C6uurVKnRHj+yfIlNB3lcT/hPt+d/Q5Pa0+823kXCCrcF7yPqLQoxriPeemrnpWFvDWtUtc7\n6DYDvsgXmDW/NjxRvz8WeowvT36Jm4Uba3utLdbhojhkgozBLoPZ88Ye+tfrz+83f2fonqGcf3S+\nXOOB2mU8LjOOgfWqzowEBRXD8+7qRgojUrMlxfA/QVxGHLsfqOsq2BnbvWBy+Of+P/wZ8CfvN3qf\nYQ2GFdiXpxgqUh9DV65LU6ummnKiVYlcJmd2+9nqxdrrv7LypzporsRr9EutFLJzs/nmzDcYKgxZ\n1nVZgRulKIqsv70eNwu312q2AGqTJqgXQ0uNqV1Br6XVbfE5t4Cpp6bSyKoRa3quKXJdrSyY6Zsx\nt8Ncfu/1OwICY3zGMOf8nHItTu99sJcaujXoaN+xwnKVBXvjZx6GjiYFFYOhjqHm7/8y8upG57yE\nbAvcRnZuNrZGtljoWxTYFxgfyLyL82hduzVftnixMIiDiQPpOekkZCW8cGxZaGnTkjU31pCUlVRp\n02ZRFMnIySAhK4GEzATiM+NJzEokKStJ82T0m5kpv5mZ8l7NNuSYW8IFdS6hvJe+jr7mfwt9C6wN\n1LWJLfQtqrwm7i/XfiEwIZCV3Va+MMs7//g8D5MeMr/D/NdqtgBoFj+fXxgtkTyvJW9TDhkZ8vX9\nzTQ1dmR1jzVaT3HRunZrdg7ayc9Xf2bjnY1ceHyB+R3na/IRlUSaMo3jYccZ6Dyw0irBFUX+8z2f\nL0pHpkOumFul8pQFSTFoCWWukr8C/6KzfWei0qMK3NzTlGlMPTWVGro1WNhxYaE3vjzf5vCU8Aop\nhvZ27Vl9fTXnH52vUNh/cnYy4SnhRKREaP6PSI0gIiWC2IzYUrvWbo6+gHlSIACZuZlk5WYV63Ei\nE2SY65ljbWiNnbEd9UzrUc+sHs6mzjiZOmk9hcDDpIdsuL2BN1zeoItDlxf2b727FQt9i1eiHGNZ\nyXOXLG+q9oOjtvHNqWl4ZGXxS6gvRk1OQ8N+2hQRUKfZmNpyKp0dOjPj7Aw+OPgB/2n6H8Z6jC2x\nTrVPqA+ZuZlV6o1UGhQyhWaN52VEUgxa4ljYMeIz43mn4Tt87/s9bhZugPrp+gffHwhLCWNdr3VF\nFuPJrxhK+zRUGE0sm2CqZ8qZyDOlUgwqUUVkSiQB8QGaEo+B8YFEZxT0sbbQt8DexB53a3dqGdbC\nXN8ccz1zzPXNMdMzw0LfAtPlHuiJIgpRRPbJCeaHH2Rb4DYGOA9gmtc0BEFAFEVyVDlk5WaRmZtJ\nRk4GcRlxxGXEEZMRQ2xGLLEZscRkxBCcFMzJ8JOaJysBATtjO1zNXWlesznNazXHzdKtQkXsl/sv\nR19Hn8nNX8x5FJsRy+mI03zU+KMqf9qsCsKSw1DIFOWq7bwveB8zzs6gmY0Xv1z8F0NRhG3vwifH\nwa5FJUirng3vHLSThZcWsvbGWi4+vsiPnX8sdpF7572d1KlRB09rz0qRqTiKWzSXy+TkqqQZw2vP\nX/f+ws7Yjra12xKfGa8pfrLj3g4OhhxkUvNJxeY/yku/XdEFaLlMTrva7TgXeQ6VqHphnSNdmc61\n6Gv4PfHjavRVAuIDNLZOuSCnnlk9Wtdujau5K44mjtib2GNvYl9yvd/8C80f7AG75nxr2wy5TM6m\nO5tQiSqmt5yOIAgo5AoUcgXGqM0OeUqxMJS5SkKTQ3mQ9IDgpGCCE4O5E3eHE+EnALUvvru1O81r\nNadlrZY0r9W81PmLrsdc53j4cT5v9nmh6cT3B+9HJaoY5DKoVOO9agQlBlHXtG6Z8z3tebCHmedm\n4lXLi5XdVmLYZ8Ozz/+3bmp35EryPDPRNWFeh3l0tO+It683b+99mwUdFxS6/nMv4R7XYq4x1Wtq\ntZgBi8sHpcxVVkmluvKiFcUgCEIfYAUgB34XRXHhc/vfA6YDApACjBNF8frTfSFP23KBnNIUqn7Z\nCE4K5nLUZSY3n0xaTho5qhws9C0ITw7nR78faVu7LaObjC52DH0dfWoa1qxwLANAB/sOHAw5SGB8\nIA4mDvg/8cf/iT9+T/y4E3dHkwbYzcKNgfUG0tCiIQ0tG+Ji5lK+mgL5lcLgVVCvM6AOupvecjoy\nQcamO5vIVeXybetvy/QjVcgVuJi/mDs/Jj2Gq9FXuRJ9hStPrrD2xlp+FdURyl0dutLDsQdtbNsU\nez2b72zGRGHCe27vFbp/f/B+mlg2qbbC7ZXN/cT7NLNuVqZj/rn/D9/7fk/r2q35qdtPz0x7T9cc\nAFjoWOnOBn2c+tDQvCFTTk3hs6Of8Yn7J3zm8VkBM+2OwB3oynQ19dWrmoD4AM12mjKtwMNVVm7W\nSz0LrbBiEARBDqwCegIRwGVBEPaIopg/4fhDoLMoigmCIPQF1gL58zZ3FUXx5Q0DLIEdgTvQkenw\nhssbpGSnAOonm+/OfYeOoMPs9rNLFRTlYOKgFcXgVMMJgGH7hqEj0yFHlYNCpqCpVVNGNxmNVy0v\nPGt6ls0bpSjOLnu27TZIHdGcD0EQmOY1DR1Bh/W316MSVcxoM6PCQWLWhtb0cupFL6deAKRmp3Lh\n8QWOhR3jWOgx/g36F0MdQzrZd6JP3T50tu9c4Mk4Jj0Gn1Af3nV7t9C/Q2Sq2rw21esVqrVQBh6n\nPiYqLQqPxqU3W+66vwtvX2/a2rZlRdcV6OvoF+zwfeKz6HZv00pXDk6mTmzut5n5F+ez9sZarsdc\nZ0nnJZjqmZKuTGdf8D56OlVRve1CyK8YotKiCrivKlVK9GQvb2EnbcwYWgFBoigGAwiCsA0YDGgU\ngyiKvvn6XwDKlynuJSQrN4vdD3bT07EnlgaWmjoMO+/t5EbsDeZ1mFfqQB8HEwfORZ4rswyiKHI9\n5jonwk9wOuJ0gYI977u9Twe7Drhbu7/4Q64oGQlw1PvZ+3cKz6UjCAJftPgCmSBj3a115Iq5zGo7\nS6sRxMa6xvSo04MedXqgzFVyMeoiR0OPciL8BIdCDmFjZMOw+sMY6joUSwNLDjw8QI6Yw7D6wwod\n72T4SYBCF6RfB/yj1bEuzWs2L1X/Hfd2MPv8bNrbtWdF1xWFz8QEAabchaVPCytVgXIw0DFgTvs5\nNK/ZnNkXZvPegff4udvPXIm+QqoytcjPtyoIiHumGJ7PRpCVm/Xam5LsgPyG8QgKzgae52PgYL73\nInBUEIRcYI0oimsLO0gQhDHAGABHx6JrG1Q1p8JPkZKdwhsubwBqzxuAG7E36OrQtUxBNQ4mDsRk\nxJS6gEdwYjD7gvdx4OEBIlMj0RF0aFGrBUO8hvAo7RGbAzbzhusblWcKyV9HoYQbgCAImnQSv938\njVwxF++23pXimqqQK+hg14EOdh34TvUdp8JPsTVwKz9d/YnV11fT26k3x8KO4WLmUmTKhnOR53Cq\n4VTpefuri4uPL2Kia1JodP7zbL+7nbkX59LRriPLui4r3txYo7Y6Qvr0IvX7Y7Oh+ywtSV00Q1yH\nUKdGHSafmMyIAyNIyU7BxcyFZjXLZirTFqnZqdyNv0sHuw6cjTyrsSTkkZWb9VKXgq3SxWdBELqi\nVgz5V4o6iKIYKQhCTcBHEIS7oiiefv7YpwpjLYCXl1f5o8C0zL7gfVgZWGmyR+YPWpnVdlaZ7Ol5\ni7ARKRG4mrsW2ic6PZqDDw+yP3g/AfEByAQZbWu3ZbzneDo7dNYEF0WnR7MlYAtHQo4w1mNseS+v\naPKvK+QPeCoGQRCY2GwiOjIdVl9fTWp2Kgs7LazUH4iOTIfudbrTvU53HiQ+YNvdbWwLVBeOCUoM\nIjA+8IX6F7mqXK5GX6Vv3crP218d5KhyOBl+kk72nUpUzFvvbmX+xfl0se/Cki5LSmcX7zbjmWI4\nswS6flclKdWb12rO1gFb6bNT7Y2nkCmqLfbkSvQVcsVcujt2VysGZUHFoMxVvt5rDEAkkN+txP5p\nWwEEQXAHfgf6iqKoyR4limLk0/+jBUH4B7Vp6gXF8DKSlJXEmcgzjGg4QvMD+zNAnRdoRMMRZXYD\nzIuUDE8JL6AYVKKKC48usPXuVk5HnkYlqmhs2ZjpLafTp26fQs9T07AmzWo243DIYe0rhtv5CvSM\n3Kk2IZQSQRD4zPMzaujW4L+X/8tnRz9jRdcVVVL719nMmRltZtDOth2fn/gcgLf3vs2AegOY0GyC\nxjPsXsI9UpWpmtxTrxtXo6+SmJVIN4duxfbbHLCZhZcW0s2hGz92/rFspo/8i9Gzzass8t3O2I4W\ntVrg/8SfgPgAfrryExObTSxRQYiiSFxmnCZeJyotisTMRJKyk0jOSiYpO4mkrCSSs5PJzMlEFEU0\n/55uAxgrjDHWNeZh0kNAHXUNsMRvCTqCjsbLLz0nXZPd9mVEG4rhMuAqCEJd1AphODAifwdBEByB\nXcD7oijey9duBMhEUUx5ut0LmK0FmaqEwyGHyVHlMKDeAECdEiPPNv1W/bfKPF7+WAZQB5ntDtrN\n9sDthCaHYqFvwcdNPmag80DqmtYtcbzeTr1ZcGkBDxIfFFj4qjA7Pny27dKjXEOMbDQSUz1TZp6b\nycdHPmZ1j9UVCuwrC1HpUQDsGrSLvcF72XxnM4dCDvFuw3f5zPMzzaKhu5V7lchT1ex9sBcDHYNi\nU3xsvL2RxX6L6eHYg0WdF5UvVuTrMLWHEsCfb8HIv8spcekJTgzG/4k/n7p/SmxGLL/d/I3ErERm\ntJ6BXCZHmavkQdIDTbxOWEoYESkRPEp9pDED52GgY4CJrgmmeqaY6priaOKIqZ4p+jr6yAQZAmpl\nk7etQkW6Mp2U7BSNYsgLIozPjGf6mekvyPvNmW9oZNmIxpaNaWzV+KUxL1VYMYiimCMIwgTgMGp3\n1T9EUbwtCMLYp/t/BWYBlsAvTzV3nltqLeCfp206wBZRFA9VVKaqYn/wfpxNnWlooV5sW+q/VLOv\nPAu9pnqmmChMOBNxhpDkEPYH7ycjJwMPaw/GdRxHzzo9yzT97FmnJ/+9/F/2PtirvaL1+U1IFXwK\nHOg8EFM9U6acnMKog6NY23NtlRRRCU4MxlhhjIuZC1NaTGFEwxGsuraKTXc2cSzsGOZ65ujL9bEz\nsSt5sFeM1OxUDoUcol/dfkV6pW24tYEl/kvoVacXCzstLH8Aob4pCDIQVRDkUwGpS8/GOxvRk+sx\nwm0ExgpjQpJD2HFvBzvu7aCuaV3CU8I1EccGOgbUqVGHuqZ16WDXATtjO/UTvbE9tY1rlzvKPikr\nCZ9QH8Z5jmOcxzjabGlD37p9Gek2UjMjWXhJ7dF/6fEl9gXvA0BXpotHTQ/a2baju2P3Uj38VRZa\nWWMQRfEAcOC5tl/zbf8HeKHw8VNPpvKH+VYjkamRXIm+wqTmkxAEAb8oP/Y82IO1gTUxGTHl8ri5\nl3CPFGUKF6Muci3mGv3q9mN4w+E0smxULhmtDa3pZNeJ3Q92M77Z+ApFCAOQli9//Kh9FRvrKZ3s\nO7G251omHJ/AyAMjWdl9Zbmvt7QkZSVhoW+hMS/YGNkwp/0chroO5dsz33IrTl0eNVeVi0z+euWZ\n3Be8j4ycjEJntKIosubGGlZdW0Ufpz4s6LigzMFvL/B9wrOHiUr2UopIiWDn/Z0AfHnyS27G3iyQ\nuuVh0kNGNBxBs1rNaGjeEAcTh0pxfvB74oeISCubVoDadV2Zq8TZzBlnM2dUoorFlxczusloPm/+\nObEZsdyMuYnfEz8uR11mxZUVrLiyAhczF95p8A4DnQeWHGCqZV6vb30VcjzsOAC96/QmR5XDvIvz\nsDWyZYz7mDKPdTPmJhOPTeStvc9+rD5v+TC7/ewK3ySHug7VpHaoMIvzeTfV1V6myua1mrOhzwbk\nMjmjDo7SVMCrLDJzM9HTeXHK3qxmM/4e9Mzc8e7+d4uNXn3VUKqUbLi9gaZWTV+oqiaKIsuuLGPV\ntVUMch6kHaWQx6dnnm2nRGlnTNSL6P5P/Fnuv5wR+0fQd9czZ4H0nHSGNRjG8q7LOTHsBHPbz0Um\nyLifeJ/O9p1xMnWqtGSNlx5fQl+uT1MrdV1zY4VxAa+k5KxkcsVcjenUysCKro5dmdZyGn8N/Auf\nt3z4ptU36Mn1mHdxHj3/7sm2u9uqNIWGlBKjnBwLO4aruSsONRzYcW8HQYlBLOuyrEzFN27E3GDV\ntVX4PvLFVM+U8Z7jiUmPYVfQLq2kLgboaN8RawNrdt3fRXfH7uUf6GG+H/es+IoL9hz1zeuzpf8W\nJp+YzJSTU5jYbCKfNP2kUrxKlCplkbMnI4URlvqWyAQZMRkxjDwwkmVdl9HOtl2h/V8l9gfvJzI1\nkm9afVPg76oSVSy4uIBtgdt4p8E7fNv6W+1Wqaudb61mSYMKzRpiM2I5F3mOM5Fn8H3kS0p2CnJB\nrlmfM9E14cibR15wZhjsMhgdmQ7fnv2WiccmsrL7Sq0nZAS1gj0VcYpWtVtpzL56cj2UqmflU+Mz\n1b+fotbUbIxsGOE2ghFuI7gRc4OfrvzEvIvzOBl+khXdiogh0TLSjKEcxGfGczX6Kt0cupGuTGfV\n1VU0q9ms1DfeiJQIpp2axnsH3uNu/F2mtJjC4TfV3kNulm7kqHI0C6QVJS8i+2zkWaLSKjDm/w14\ntl1JT1pWBlas672O/vX6s/LqSr45+02ps7iWBVM9U5Kyir45JWUlMch5EDsG7sDOxI7xx8Zz8OHB\nIvu/CmTnZrP2xlrcLNzoZN9J056jymHWuVlsC9zGR40/YkbrikelF8rMfGbI6LulPkwURe4n3Gf1\ntdUM3zecrn915btz3+H/xJ8ejj1Y2mUpZ4afoZtjNwQENvXdVKSHW/96/Znbfi6Xoi7x+fHPK1wZ\nrjDuJdwjMjWygMeXXCYvkGJboxgMSna2cLd257devzGzzUx8H/ni7eutdZkLQ5oxlINT4adQiSq6\nO3Znw+0NxGXGsaLbihKfbpOzk/n9xu/8GfAnckHOWI+xfNT4owKLgPljGZ4vB1hehrgO4bebv/FP\n0D+M8xhX9gHCLj7brmS3Qz25Hgs6LKCeaT1WXl1JeEo4K7quKFcG0KKoaVCT6PRoRFEs9DMTEZEJ\nMmoa1mRDnw18fvxzvjr9FXEZcYxsNLKQEcvH1rtbaVazmcZ5oTLZeGcj4SnhrOmxpkDJ0q/PfM2R\n0COM9xzPp+6fVp7fvzzfreaX1sV+j0RR5G78XXxCffAJ9SEkOQQBAQ9rDyY2m0hHu440tGiokTU+\nM56td7fSp26fEr3vBjoPRCWqmHluJpNOTGJlt5VajSc4Hn4cAYHODp01bTqCTgEzUJ5iMNcrXaoO\nQRAY1mAY4SnhbLyzkUnNJ5W5bGpZkWYM5eB42HFqG9XGysCKDbc30KtOr2JTZeeoctgSsIX+u/qz\n4fYG+tXtx74h+xjvOf4Fz5DnXVa1gYOJA21rt2VH4I7iC78XxR+9tCZLaRAEgTHuY1jaZSn34u/x\nzt53tFqVrrZxbZQqZZEzKAFB45deQ7cGa3quobtjd/57+b8v1rQuJ49SH7Hw0kIOPDxQcucK8iTt\nCWtvrKWbQzdNOdms3Cwmn5zMkdAjTPWayliPsZUfDJbfBJldsHqZKIrcir3FUv+l9NvVj2H7hvHH\nrT+oZVSLmW1mcnzYcTb128QY9zG4WboVkHXDrQ1k5WaVOl5nsMtgfmj3A76PfPn27LfF1gcpKyfC\nTuBh7VHgQUYuk5MjPqu98DjtMUCZb+7tbNuhElWEJYdpR9hikGYMZSRdmY7vI1/ebvA2v1z/BaVK\nyaTmkzT783yb875sd+Lu4O3rTUB8AK1tWvOl15e4WboVOX4tw1royHS0qhgAPmz8IZ8e/ZT9wfsZ\n4jqk9Afm5DPllDLCWVv0rNMTRxNHppycwujDo/mixRd80OiDCt/A8nLzX4m+Qn/j/i/s19fRL1BC\nUk+ux5LOS5jlO4tfrv+CYw1H+td78biysCVgCwICIxqOKLlzBRBFkTkX5pCrymVqS3VCwOTsZCYd\nn4T/E39mtZ3F2/XfrlQZNOQ3Qc63Be8kwpPD2fdwH/uD9xOaHIqOoENr29Z84v4JXR26lpgALy4j\njm2B2+hbt2+ZUr8McR1CUlYSS/yXYG1gzVctv6rw9+px6mMC4gP4osUXBdrlgjp+Io/I1EhMFCZl\nXkd8lPoIoEqSAkqKoYxcfHyRbFU29UzrMe/iPN5t+G6BQt953i7JWcksDVzKxjsbMdc3Z2mXpfRw\n7FHil08uk2NvbK91xdDWti0NzBuw4fYGBrsMLr0deW6+6l7VkF6ggUUDtg3Yxqxzs/jR70f8ovz4\nof0PFQqGq29eH2OFMX5P/Aq9wdc0rKkJTMpDLpPj3dabyNRIvvf9njo16tDEqkm5zp+mTGPn/Z30\nrNOz0k0CO+7t4FTEKb5u9TUOJg5EpUUx7ug4QpJDWNhxIf3qab/iWrFMvELiKi8OGxmy98BIrsdc\nR0CgpU1LPm7yMd0cu5WpJO3vN39Xzxbcyx7dP6rxKJ6kP+HPgD+pZViLD5t8WOYx8nM8XO2p+HxE\n+fNrDBEpEdiZ2JVJEYmiyN/3/qauaV1czFxKPqCCSKakMnL+8XkMdAy4HHUZXZku/2laMDzDQK72\ndBi+fzjrb6/nDZc32P3GbnrW6VnqL4K9ib1W0m/nRxAERjUeRXBSMGcizpR8wPN8Wn1ZSkx0TVja\nZSnTW07n3KNzvLnnTc5Gni33eHKZnLa2bTkWeqxQ01otw1qFmpkUcgVLuyzFUt+SSccnEZMeU67z\n/xv0L6nKVN5v9H65ji8twYnBLL68mHa27Xi34bvcS7jHewfeIyotil97/FqlSiErN4sjIUeYeH05\nXR3tmGtlQVrcfSY3n8yRt46wrvc6hrgOKZNSeJj0kG13t/Gm65tFJkMsDkEQmNZyGr2derPEfwn7\ng/eXeYz8nAg/QT3Tei/IoiPoFCjjGZkaqUl/U1r2P9zPrbhbjHQbWSX5nyTFUEbOPzpPTcOa+IT6\n8HaDtwvYEtOV6Sy6vEjzfl2vdXi38y7zlDFvxiCK2s0V2KduH2yMbFh/e33pDgi//Gy7dvXGIQqC\nwMhGI9nafytmemaMOzqOBRcXFDD5lIWhrkNJyErQPOXlx9XclXsJ9wpM//Ow0Lfgp24/kaJM4YuT\nX5TZtzwzJ5N1N9fRvGZz3K0rL+VGYmYiE45PwFBhyJz2c/B95Muog6MQRZENfTZokj5WJipRxeWo\ny3j7etN1e1e+PPUlt2Nv815yCn9HPmbXg7t83PTjcs+alvgtQV9Hn/Ge48sto0yQMb/DfFratOS7\nc9+Vey0rNiMWvyi/Qj0TZYJMM2MQRVGtGExKrxiepD1hwcUFeFp78qbrm+WSr6xIiqEMRKVFEZIc\noraFynT4qPFHmn33Eu4xfP9wwlLUC0NLuyylVe1W5TqPg4kDqcpUErO0a9NXyBS87/Y+/k/8uRFz\no+QD1pUvD1JlkmdaGuk2ki13tzB0z1DOPzpf5nHa1m6LrZEtWwK2vKCAPaw9yFZlcze+cLfKBhYN\nmNlmJtdjrrPnwZ4ynXd74HZiMmKY2GximWUuLcpcJVNOTSEqLYoVXVdwOOQw44+Nx87Yjs39Nr+Q\nTVbbPEh8wIorK+izsw+jD4/mwMMDdHXsytqea/F5y4epE0NokK2kIs+95x+d51TEKT5x/6TQsqxl\nQVeuy/Kuy7EztmPKySnlcus++PAguWJuoaZJmSDTrDnGZsSSlZtVao/DrNwsvjj5BUqVkjnt51Ra\nUN7zSIqhDOS/Ab1V/y2sDa0RRZEd93YwYr86B/zXrb4GqJCnQ96aRZ6S0SZv1n+TGro1WH29DN41\nU1+u6F89uR7TW01nfe/16Mh0GOMzhpnnZhYbm/A8cpmcj5t+zNXoqxwLO1ZgX/NazREQOPuoaHPV\ngHoD8LD24KerPxVItV4c6cp01t1cR9vabYut/10RclW5zPSdyeWoy3zX5jv+DfqXRZcX0dWhKxv7\nbqy0XFQx6TFsvL2RYXuH8cbuN1h/az3OZs4s7LiQk8NOMq/DPNratlXf2PKbQg6+mFiuJHJVuSz2\nW4ydsR0j3bTjPlxDtwYruq4gIyeDKSenlDl+Zu+DvTSybFSou2xeBUWAiFS1ibg0MwZRFPnB9wdu\nxt5kQYcF5TKXlRdJMZSBPMWgkCkY3WQ0KdkpTDs9jdnnZ9O8ZnN2DNxBZ3u1/3JFgmfyisNUhlua\nkcKI0U1GczbyLP5P/IvumN+MYlyz6H7ViJeNF38P/JuPm3zM3gd7GfDPAP4K/KvU5p2hrkNxMXPh\nR78fC3xeVgZWtLRpyYHgA0Wa8wRB4KuWXxGbEcu6m+tKdb4NtzeQkJXAhGYTStW/rOSqcpl5bib7\ng/czrP4w/r73Nzvv7+STpp+wtMtS7ZRyzUe6Mp29D/Yy1mcsPf7uwWK/xcgEGdNbTufo20dZ3WM1\n/ev1L/68F38tel8R7Araxf2E+0xpMUWrMQjOZs7M7zCfm7E3mXthbqlNuUEJQQTEBxRZlCt/pH3e\n2mFpZgwrrqxgb/BeJnhOoHudCmQtKAeSYiglKlHFwRB19OtQ16GkZKfwzr53OBp6lEnNJ/Frz1+x\nMrDSZFVNzymf7RvUawxyQU5Icog2RH+BEW4jsDawZsWVFUV/+efWqpRzaxt9HX0mt5jM9gHbcTZz\nZs6FOQzfP7x4pfcUHZkOX7f6msjUSE22yzz61+tPSHIIV6KLtjm7W7vTr24/Nt7ZyOPUx8WeKyw5\njDOCsqEAACAASURBVHU319G3bt9KWVtQqpTMPDeTvcF78bT25HDoYR4mPWRpl6V83vxzrUUzK1VK\nToWf4qvTX9Hlry58e/ZbHiY95OMmH7N78G61ma/RyJIDEqcFl+v8SVlJ/Hz1Z5rXbE7POj3LNUZx\ndK/TnU/dP+XfoH81BZ1KYm/wXuSCvMjCTjmqHE3eqYdJD5EL8hIVw+83f2fdrXUMqz+sXPnXKoqk\nGEpJXn51gEaWjXj/wPtk5GTwR+8/+E/T/2h+eKa6aq+K5Kzkcp9LIVdgZ2xHaHJoxYQuAgMdA8Z6\njOVq9NWik+vluddZVr5rnDZoYNGA9b3Xs7jzYhKzEvnw0IdMPD6RwPjAYo9rXbs1/2n6H3be38nu\noN2a9j5OfbDQt+CXa78Ue/zk5pNRqpTsuLejyD6iKDL/0nwUcgXTvKaV7cJKQVJWEuN8xrE3WF0U\n5lrMNWwMbdg+YLtWbp4qUYX/E3/mnJ9Dt7+6MeH4BHwf+TKw3kDW917PwTcP8nnzz6lnVoYSskbl\nWxdY5r+MpKwkpreaXmneOZ95fkZn+84suryoQN3mwlCJKvYH76e9Xfsi1zryK4agxCDq1KhT7Ezn\nr8C/WHFlBf3q9mNGmxnVUoVOUgylxPeRr2Z7zvk51DKqxeZ+m2leq2AxdYVcgbHCuMILx441HCtN\nMYA6wMfRxJEVV1cUvx7y2cWi971kCIJAH6c+7HljDxM8J+Af5c/be9/mq1NfFVDszzPeczytbFox\n+/xszkWeA8BQYcgnTT/hUtSlYl1jaxvXpqVNS3xCfYqcfR0NO8q5yHNM8JyAtaF1xS7yOUKSQhh5\nYCQXo559Tm+6vsmf/f4sEF9TVkRRJDA+kKX+S+m9szcfHvqQvcF7aWvblp+7/cyJt08ws+1MvGy8\nKj4buVA6c9LlqMvsvL+TDxp9UKmp2WWCjLnt52KhZ8FXp78q1vPtctRlnqQ/Kba2e0ZOhsaScD/h\nfpFle0Gd6HDuhbl0tu/M3A5zKydvVSmQFEMpye+G6mXjxca+GzWlIJ/HTM9Mkw+lvDjVcCI0OVTr\nLqt5KGQKJjSbwP2E+8WnZZC/ejGQBjoGfOrxKQffPMjHTT/mZMRJ/p+98w6L4uri8DsUlSIgoIJG\nxa6AigrWGLsSGxpbYqJoYmwxauyfGiW2aNQkatTEiiWJvSs2sPeGBRUVpCm9d1j2fn+sLCAgZVdK\n9H2efZjduXPnLrs7Z+495/xO30N9mXp+Kg/DHmZrr6WhxYr2K6hlVIsJbhOUs6iB9QdiYWDBvCvz\niErK3dB3t+iOT4wPTyOfZtsXmhDKgqsLaGjckM8bfK629yiEYN/TffQ/3F+55GhSzoTVnVbj1Map\nUIWi5ELOvdB7/HrrV3od6MWAIwPY5rGNukZ1lU7kXz75hfbV2heszGdenMjbAZ0kS+Knqz/xkf5H\njLUphN5XATEqZ8SidovwjfFl2a1lubY77HUYfW19OlTrkGubRFkiulq6JKQmEBAXQF2jnA3DOf9z\nzL40G1szW0UpVVXrp6jAB8OQDzLHs39W9zPWdllL+TLlc21vXM5Y5RlDDYMaJMoSCU0sXBJVfuhu\n0Z0Gxg1YfWc1ibLEjB0phfePlCQMyxoysdlEXD5zwdHSkcsvL/PFsS9wdHHkrN/ZLDMlo3JGbOy2\nkdpGtZl0dhJ7nu6hjEYZln6ylIikCOZemZurU7tz9c5oSpqc9DmZ5XW5kDPn8hwSZYlqrW8QnhjO\nhLMTcLrqRIpckaDXrUY3DjgceOsFKidS5alcfXWVhdcW0mVPF746/hXbH2+nWvlqSo2itV3W5u1E\nLgwVLPLddP399fjG+DK39dx3IpedE63MWzHcejh7n+7F1dc12/7o5GhO+pzEvqb9Ww1xgiwBXW1d\nvKK8AKhTIfvy7OWXl5l8bjINjRuyutPqQhl2dfLBMOSBTC6j2Y6M5SKn1k55WnKjckZEJkWqdN70\nZYB3uZykIWkw3W46r+JfseH+howdzqrpAJU0THRMmGw7mdMDTjPNdhqB8YFMODsB+332rHVfy8u4\nl4DCkGzotgHbyrbMvzqfWZdmYWFgwVTbqZz1P8v8a/NzXHYzLmdMC7MW2QoMbX+0nSuvrjDNbppa\nam6npqWy1WMrHXZ3UNYWN9Mz4/eOv7O8/fJ8a+jEp8bj6ufK7Euz6bCrA6NOj+Kw12FsKtnwc7uf\nOT/4PH92/ZNB9Qe92zrco87nq5lnhCdbHm7BobYDrau0fnfjyYHvbb7H0sSSeVfnERwfnGXfwecH\nSU5L5vP6b58JJqYmoqOlw7MoRdh3PaN6WfZfC7zGxLMTqW1Umz+7/lnk1dpyovStExQhafI05l6e\nq3y+ufvmfDmCjMoa5bisUBAsDCwA8Inxwc7MTqW+3oadmR29avXC2cOZPrX7KGKlX6lPybQkoV9G\nn2FWwxjScAhn/M5w4NkB/rz3J+vuraOleUscajvQvlp71nVZx4YHG1jrvpa7IXeZZjeN0Y1H89f9\nvxSSza1+zOY8bFyxMdeDrisdjXdD7vL7nd/pVK2TyiJ1afI03PzdmHd5HrGpGZXARjcezTeNvsnz\nDlou5HhGeHL51WWuvLrC3ZC7yOQyDMoY0KFaBzpX70zrKq2L7E5ciY5Rnk3S5Gk4XXHCoKwBU22n\nFsGgsqKtqc3SdksZeGQgi64vYlWnVYDif7rbczdNKzV9a8KgEEIxY9DS5VnkM3S0dLLUEr8ZdJPv\nXb+nWvlqrO+6vkCSIO+SD4YhF+RCzk9Xf1JGegD5DjM0Lmf81jXp/GCmZ0YZjTL4Rr+7GUM6U2yn\ncM7/HD/f+Jk/u/ypUkZqaUBLQwt7C3vsLewJjAvkkNchDj4/yKxLs9CStLAzs6NT9U4sabeEDQ82\nMOnsJFqataRd1XYcfH6QZ5HPWNFhRZaQQ3M9c+RCTmhCKDIhY6LbRKrqV2V+2/mFjipJkiVx2Osw\nK26tyBL+3Kd2H8Y0HkM1g2o5HicXcp5FPuNW8C1uB9/mdvBtpc+rfoX6DLMcRtsqbWlauWmxrmPn\nh40PNvIw/CG/fPILRuXyNiTvAgtDC8bajOW327/h6utK5xqdufrqKn6xfnnKccSnxpMm0jAsa8j9\nsPvUNqytdCjfDbnLd67fUUW/Chu7bSwS1dT8ohbDIEmSPbAS0AQ2CiGWvLFfer2/B5AADBdC3MnP\nscWBEIKF1xZy4PkB5Wvmeub5LqlnXM6YpLQk4lPjCz0t1JA0FJFJse/eMJjqmDK+6XiW3FjCad/T\nKKsv5FIJ67+Eub45Y5qMYVTjUTwIe4Cbnxtufm4sur4IgNqGtdGUNLNE/XiEe9D7QG9GNx6No5Uj\n5bTKYa6nyCh+GvmUFbdXIEfOms5rCnwHKBdy7obcxeWFC7s8d2XZZ29hzzibcdQ0rJnl9YikCB6G\nPcQjzIOH4Q+5F3pPmQVurmdO2yptaWHegrZV2qo9Kupd4h7izrp76+hRs0euOQJFxVDLoRz3Ps7i\n64tpYd6CnZ47MS5nTJcab5eNiU5RfA4GZQx4FvlMWT3vfuh9xp4ZS2XdymzstlFlWQ91o7JhkCRJ\nE1gDdAUCgJuSJB0WQjzK1OxToO7rR0tgHdAyn8cWOX+4/8Gep3twtHTkqPdRwpPC+bjqx/k+vrKu\nIjksKD5IpbXlGgY18I4uXCJQQRlcfzAHnx9k6c2lfCxJ6AoBtiPyPvA/goakQZOKTWhSsQmTmk3i\nRfQL3PzduB54nZdxL0lLy+p4TpWn8of7H/zh/gfDLIcpM97Hu41HS0OL9V3XKzPY8yI4Ppg7IXe4\nFXSL3U93Z9vvaOnIoPqDqKhbkRfRLzjidQTvaG+8oryUpSRBUQuklmEtOlXrhK2ZLbaVbXONnCvp\nxKXEMfPiTMz0zJjTak5xDwdtDW2c2jgx5NgQ/nfxf1x8eZFvrL/JM/M63UAnpyUTkRRBA+MGeIR5\nMOb0GIzLGbOx28YSaazVMWNoATwXQngDSJK0E3AAMl/cHYBtQhF7eU2SJCNJkswBi3wcW6S4+rmy\n/v56+tbpS/PKzdn6aCtAgcovpqtFqsMwnA84nyVB5l2hpaHF7JazGeoylD8qGDI9IgoqvvuSkyUR\nSZKoZVSLWka1GNloJKlpqXiEe3Ar+Ba3gm5x+dXlLO23PdrGtkfblM9lchn7n+3nbshdzPXM0dXW\nRVtDG01JkyRZEgFxAfjF+PEs6hl3Q+7mOg6jskY0qdhEOYMITQxVVpbTkrSoYVADKxMrBtcfjLWp\nNZYmliXCcakOFl9fTGB8IM72zm+NACxKrE2tGdJwCH8//hsgX76jdMOQHkRSVrMso06PwqCsAZu6\nbaKyXslUGFDH1aYqkLmqTACKWUFebarm81gAJEkaBYwCqF698Ik7b8M72pvZl2ZjbWLNnFZzmHo+\nw9lVEEXKzIZBFSwMLJDJZbyKe6VSslJ+salkw+D6g9nxZCed4xNpnklD/n1GW1Mbm0o22FSyUdbf\niEiKwDPCkwPPD+DywiXbMUe9j6p83iRZEr4xvpjpmdG2aluq6FehtlFtahvWpppBtRLvHygsx7yP\nccT7CGObjKVppabFPZwsjGo8SmkY8nNRT49OTDcMK26tQL+MPpu6b3pngobqoNQ4n4UQ64H1ALa2\ntmrP+opLiWOi20TKapblt46/EZMcoyxoIyHlmpSSExV1KyIhEZSgmmFIX0v2ivIqEsMAMLn5ZC4/\n3MGcisbsiw5AzZHr/xmMyxnTukprmlVuRkxKjDJjOl17yeWFC2GJYW/tQ09bj3oV6mFb2ZY6RnUo\nX6Y85cuUx6CsARXKVsCorFGxyCEUJwGxASy8thCbijbFohGUF5mVeF1euORZ4jU9Dyl9lqmrpcvm\nbpvzLbtdXKjDMLwEModHfPT6tfy00c7Hse8cuZAz+9Js/GP92dBtA2Z6Zmx6sIk0kUYdozrI5LIC\nJfdoa2hTUadinsJqeZFews8r2ouOdFSpr/yiq63LwtAIRphXYoXPQX6k+Nd3SyoRSRFMdJuIe6g7\nHat15Kz/WRqbNubLhl8y3W56cQ+v1JGSlsKMC4osaHUmBKqLNHkazg+dsTSxRAjBqjur6FKjy1uD\nUtJvDtLzXzZ135RrNFlJQh0JbjeBupIk1ZQkqQzwOfBm9ZLDwDBJQSsgWggRmM9j3zl7n+7Fzd+N\nKbZTlDkDLi9csKloQ6IssVCFTcz0zVSeMeiX0cdMz4znUc9V6qegNE9OxjE6lt2ayco74Q9kxSvK\niyHHhvA44jHL2y9XOp/zVBX9QK4svr6Y+2H3md92foEqnBUVrn6u+MX68Y31N0y2ncyr+FfsfPJ2\nBdbM6rzjmowr0poKqqCyYRBCyIDxwEngMbBbCOEhSdIYSZLSK3QfB7yB58AGYNzbjlV1TAUhPDGc\n3+/8TguzFsqiH74xvnhGetKmShtexr0skOM5HTNds2yZkoWhtlFtnkcWrWEAGB8VRa2UVOZemVug\nAjjvA1deXeGr41+RJEtiS/ctdLfojm+sL5qSZokLOywt7Hm6h33P9jGy0ch3IqetKkIINj/cTPXy\n1elcvTOtzFvRtmpb/rr/V66/j4DYgCyVEh3qOBTVcFVGLZIYQojjQoh6QojaQohFr1/7Uwjx5+tt\nIYT47vX+RkKIW287tij57fZvJMoSmd0yQ942XdogXdOklmEB5IRfU0W/Cq/iXqlUyQ2gjmEdXkS/\nKHBtYVUpK2BxaDjhieEsvr74nYn5lSbS5Gmsv7+ecWfGYa5vzr89/6VRxUYAXHp5iWaVm6m1cMx/\nntffKfeyZVh8fTFtq7RlvM27KWKkKjeCbuAR7oGjlaOyvObk5pOJS4lj44ON2doHxgUy8tRI5XNT\nHVNlrktp4L3WSrobcpdDXocYZjksi5b8KZ9TNK7YmJQ0hUBZfuPRM1OtfDVS5CkqzxrqVKhDijwF\n/1j/vBuri+8V01+rlBTGNBnD8RfHOfj8YNGdvwQSHB/MqNOjWH13Nd1qdGObfUaZzMC4QEXyUtVP\ninmUpYyrawjT1GBKJVPMdM1Y+snSIqtpXFC2PNyCSTmTLHf99SrUo0etHuzy3JVl1hAcH8w3p77J\n8lpj08alKpDgvTUMMrmMhdcWYqZnxujGo5Wv+8f68zjiMd1qdMMvxg8JqVDrnenGRNXMZaUD+rUy\nY5FgkpF78W2jb2lp3pJF1xeprP9UWjnvf54BRwbwIOwB89vMZ+knS9HPlBV+8aUieu2Tah8MQ0FI\nPTWbKZVMidXQ4PeOv5cYnaA3eRLxhMuvLvOV5VfZHM1fW39NoixR6WsITQhl5KmRRCRFsOjjjAWQ\n9JllaeG9NQwHnx/kaeRTZtjNyBJxlL6M1KVGF3xjFTHk+ZXCyIzSMKiodZS+jFXUDuh0NDU0WdJu\nCeXLlGfq+alvLVryXyM6ORqnK06MdxuPmZ6iIlq/uv2y3fmdDzjPR/ofUdOgZi49feBNhBAsManA\nnXLl+CnNsFABHkXF5geb0dXSzTGhrV6FerSr2o5/nvzDy7iXjDw1kuCEYP7s8mcWZVrbyrZFOWSV\neS8NgxCCXZ67qF+hPp2rZy2yfcrnFFYmVlTVr4p/jH+h8wcq6VairGZZlWcMutq6VNWvWrQzhsys\nbIKpjilL2y3FN8aXBdcW/Of9DUIITrw4gcNBBw4+P8gI6xH83ePvbBpFoEhivPrqKh2rdyxVSwXF\nzVaPrew2KM+IqBg+HZFLedkSgHeUNyd8TjC4weBcZzRfW39NRFIE9vvsCYwPZG3ntdhUslFKlQBY\nmVoV1ZDVwntpGB6GPeRJxBMG1huY5ccckhCCR7iHUhjLN9aXGuUL7l8AhfZOtfLV8IvxU3m8dY3q\nKrXci5xIHwBamLdgTJMxHPU++p/2NwTGBTLebTzTLkzDTM+Mnb12Mrn55FydyhsfbEQglBFtH8ib\nkz4nWXF7Bd3j4pkUGVWiqwSuu7cOHS0dRljlrhuWuVTn7x1/x9ZMMTtINwzNKjUrdVnq76Vh2P10\nNzpaOtmyFtNj9ttVbUd0cjTRydEqZRzXMKihlkI7DUwa4B3tXbTLOF/syvbSqEajlP4GzwjPohtL\nEZCQmsBa97U4HHLgZtBNpttN5+8ef781VDkoPoj9z/bTt07fUitWV9S4h7gz6+IsbORaLAoLL9EX\noGeRzzjpc5IhDYfkKokdkxLDqNMZGdqxKRn1Mm4H3wZQKqqWJkry5/JOiEmJ4cSLE/So2SOLAxEU\n8emmOqbUq1BPeadfvbxqhiEgLgCZippDViZWimIrkUV4Ma5vn7H9OlQ23d9gWMaQiWcnqlxzoiSQ\nJk/jwLMD9DrQi3X31vHJR59w0OEgQy2H5hkhs+nBJoQQSv2kD7wdvxg/vnf7HnN9c1b5+1C2hK9I\nrru3Dl1tXRwtHXPcH58az9jTY3ka+ZQ/Ov2BmZ4ZB55lSPVfeXUF4J0W2npXvHeG4Zj3MZLSkhhY\nP6sjKU2expVXV2hTpQ2SJBGcoAgzVUXoKrMInipYmlgC8Ci8mERn52c40Ux1TPmt42+EJIQw/cJ0\nlY1ecXIt8BqfH/ucuVfmYq5nzvZPt7O8/fJ83f0HxQex79k+HOo4lHjdm5JAZFIkY8+MRUJibee1\nVJC/zu+Zq1oJ3HeFZ4Qnp31P81XDr3IsEJSclswEtwl4hHuwov0K2ldrj0NtB668ukJQfFAWP1z6\n77c08d4ZhuuB16lWvhpWJlmdQc+inhGTEkMr81ZAhviVKhIH6bkRqkYUVdKtREWdiniEFWlSOOTi\nbGtcsTE/tvqRq4FXWXlnZdGOSQ3cCrrF1ye/5ttT3xKTHMMvn/zCjh47sKlkk6/jhRDMvzofDUnj\nw2whHyTKEpngNoGg+CBWdVpF9UurM3ZqlMxL0Fr3tZTXLs9Qy6HZ9qXKU5l2fho3g26y8OOFdKre\nCVBkNgsEh54fUt5YAiVO8yk/lL4Rq8izyGc5rhunrwemh5WFJYahIWlQoWzhy+3VNlTkAzyPeq78\n8hQWKxOrop8x/M8PnF4bh5R4KJOh9d+vbj88wj1w9nCmoXFDetTqUbRjKwR3gu+w1n0t14OuY6pj\nyswWMxlQb0CBw5H3PN3DxZcXmdliZonU9ClJpKSl8MPZH7gfdp/l7ZcrjO+N9sU9rLfyKPwRbv5u\njLMZly0SSS7kzL08l7P+Z5ndcja9avVS7qtWvhotzFpw8PlBZf3svNRXSyol01y/IxJSE/CP9ade\nhXrZ9t0Ovk0VvSrKpaOwxDBMypmolImpX0afKnpV1JKDYGliWfQO6Mwszr68MsNuBs0qNWPelXk8\niXhSDIPKGyEEN4Nu8u2pb3E84cjzqOdMt5uOy2cufNnwywIbBZ9oH5bfWk5r89Z80eCLdzTq/wYy\nuYyZF2dy+dVlnFo7KTSQMoc6zyuZPqp17uswKGOQLdJMCMHP13/mqPdRJjSdwOcNPs92bN86fQmI\nC2DZrWUADLMcViRjVjfvlWF4HvUcgchmGIQQ3Am+Q7PKzZSvhSWGqUUps06FOmoxDFamVggEjyMe\nq9xXgei/Kddd2prarOiwAsOyhkx0m6gsOF8SSJOnccb3DF8e/5KvT37N08inTLWdikt/F4ZaDqWc\nVrkC9ymTy5h1aRbaGtosaLtAWdT9A9mRCznzrszjtO9pZtjNoF/dfoodP2Vary+BeR93Q+5yLuAc\nw62GZ6sc94f7H+z03Mlwq+G5LiF2qdEFfe2MoJbS6F+A98wwpEs6vGkYghOCCU8Kp5FpRtp6aEKo\nWgxDbaPa+ET7kCpPVamfYnNANxqQse2U3edgqmPKyo4rCU8KZ/K5yaSmqfY+VSU5LZm9T/fS91Bf\nfjj3A5FJkcxpOYeT/U/iaOWonOIXhjXua3gQ9oAfW/1YYksylgSEECy9sZTDXocZZzOOryxzyPHo\nsbzoB5YHQghW3FpBRZ2KfNnwyyz7tnpsZf399fSv25/JzSfnmsyoo6VD88rNi2K475T3yjC8iH5B\nOc1y2aJOHocr7sIzW/fwxHC1GIa6RnVJlafiH6OaCJ6pjimVdCvhEV7EDuh8YGVqxU9tfuJ28G0W\n3ygeJdbg+GDWuK+h+97u/HT1J3S0dFjWfhlH+x1lcIPBhZohZGa35242PthI/7r9sa9pn/cB7zGr\n767mnyf/4GjpyJjGYzJ2ZL6xaPFt0Q8sD9z83LgXeo9xNuOyyOTse7qP5beW061GN35s9WOeGe7p\nN4Gq3IQUN++V87mMZhlkchkSWT/YxxGPkZCUM4k0eRrhSeoxDOkieM+inmVRcC0MliaWRR+ZBOAU\nnfGjdjJUPH+DnrV68izyGZsebqJehXpFsv4uhOBG0A12ee7Czc8NuZDTtmpbHK0caWnWUm0SFWf9\nzrLo+iLaVW3H7Faz1dLnf5UtD7ew4cEG+tftzxTbKTl/Bhbtin5geSCTy/j9zu/UNKxJ3zp9la+f\n9j3N/GvzaVu1LUvaLcmXz/Fh2EOAUiWz/SbvlWEwKmuETMiIT43Pktz2JOIJFoYWyruEuNQ40kQa\nRmWzxy8XlJqGNdGQNHge9ZzudFepr0amjTjnf47o5OgSqUQ5odkEvKK8WHpjKbUMa9HSvOU7OU9s\nSiyHvQ6zy3MXL6JfYFjWkGGWwxhYfyDVyqu3bKJ7iDvTL0zH0tiS5e2Xlzppg6Jkt+dufr39K59a\nfJr9zjrzbGH40aIfXB7sf7YfnxgfVnZcqQwvvRl0kxkXZtDItBG/dfgNbc28P/tUeSoxKTEAhCeF\nv9Mxv0veq6Wk9ItpVHLWaAi/GD8sDCyUz+NT4wGyOZ8KQzmtctQwqKGWqJ2mlZoCiotVkZN5lpCD\nrwEU+lA/t/sZCwMLppyfovLy2Zt4Rngy/+p8Ou/pzJIbS9DX1mdh24WcGXCGybaT1W4UvKO9Ge82\nnkq6lVjTZU2B6n6/bxzzPsbCawtp/1F7FrVblPXOOvPSok3J05RKSE1g3b112FS0oWM1RW31JxFP\nmOA2gWrlq7Gm85p8LwvdDb6r3I5OjlZLFcfi4P0yDGUUF7TMBTTkQk5AXEAW6Yt0w6CnrYc6aGDc\nQC2GoZFpI7Q0tLgdclsNoyoE9T7N2Jal5NhEv4w+qzspEpi+d/ueuJQ4lU6ZmpbKce/jOLo4MuDI\nAA57Haa7RXd29tzJPz3/waGOg8r+g5zwjPDkm5PfoClpZpNQ/kBWzvqdZfal2diZ2eU8q8ocidR3\nTdEOLh9se7SNsMQw5dKXf6w/Y8+MRU9bj7+6/lWg2Xm6bH8VPYUf88LLkqsc+zbeK8OQntqeecYQ\nmhBKclpylrvNdMOQOexMFSyNLQmKD1JZW6icVjmsTKyy3JUUKUMyFT5fWDHXZtUMqrGi/Qp8YnyY\neXFmocqSBsYFsurOKrrs7cKMizMITQxlqu1UXAe6sqDtgncqY3wn+A4jToxAQ9Jgc/fNVDNQ70zk\nv8S1wGtMPT8VSxNLVnVald1Ie7pkbI+7VrSDywfhieFsebiFTtU6YVPJhvDEcMacHkOqPJX1Xddj\npmeW777S5Gns9FT8Rr6y/ArjcsbFM7tXAyoZBkmSjCVJOi1J0rPXf7OlCUuSVE2SpLOSJD2SJMlD\nkqSJmfY5SZL0UpIk99ePd5o+m+4MyixG9ypeoWNUtXyG3k16EpmOtnqiChqYKDKt1ZGD0KxyMx6G\nPyRJlqRyX4ViaqacjC25f1wtzVsyo8UMzgec5w/3P/LVtVzIufLqChPdJmK/356NDzbS2LQx67qs\n42i/ozhaOb5z38qFgAuMPj0aEx0Ttn+6ndpGtfM+6D3FPcSdCW4TqGFYg3Vd1uU8w/43UxJYpYZF\nN7h8su7eOpLTkpnYfCLxqfGMcx1HSEIIf3T6o8DBIndC7ii3m1ZqirWpdfEEi6gBVWcMMwFXIURd\nwPX18zeRAVOEEJZAK+A7SZIyZ338JoSwef04ruJ43oqZnhmNTRvj8iLjLib9Lj6zrK5MKIThriCm\ndAAAIABJREFU1OVobGis+EGowzA0r9QcmVzGg7AHKvdVKPQzzRR8L+e6pATwef3PGVBvABsfbOSY\n97Fc20UnR7P90XYcDjow+vRo7obcZYTVCFz6u7C682o+rvpxkSSTHfE6wgS3CdQyqsXWT7d+kNJ+\nC54RnoxzHUdFnYqs77o+Z4Od2ReVQyRbcfM08il7nu5hYL2BVNOvxqSzk/CM8GRFhxX51s3KzIkX\nJ5Tb9Y3rY21iXbxqBSqg6q/NAdj6ensr0PfNBkKIQCHEndfbscBjoNjkKHvU6sGTiCd4R3kDEJ2i\n+MIalDFQtkmPQ1aX+JVhWUOq6FXhSbjqfoZmlZuhIWlwLbAYp+WZf+RvWVKSJIlZLWbRvHJz5l2Z\npwzjS+dx+GOcrjjRZU8Xfrn5C4ZlDVn88WLODDzDpOaTiky1VC7krL+/nlmXZmFb2ZbN3Td/8Cm8\nBZ9oH0adHoWeth4bum3IOaz7yMSM7bdkzxcXQgh+ufkL+tr6jLUZy+xLs7kWeI2f2vxUqPoJMrmM\nM35nAIXMtraGtlKtoNhUkVVAVcNQWQgR+Ho7CHhrOqgkSRZAU+B6ppe/lyTpviRJm3NailI33S26\noyFpcPyFYnISk6wILct8x5MuJa0lqS+at4FxA7XMGMqXKY+1qXXxGgaAWYEZ27lEKYFCNuPXDr9i\nUs6EiW4TeRn3kiNeR/jy+JcMOjqIY97H6FmrJ7t77WZHjx30rt0712pp74LYlFgmnZ3E6rur6VGz\nB2u6rFFb0MF/kcC4QL49rUhOW991fc6zqtQkuO2c8Txz9nwJ4az/Wa4HXmeczTjW31+Pi48LPzT/\nAYc6DoXq70bQDaUkTGvz1gBKBeeSmJSaF3kaBkmSzkiS9DCHR5b/oFCku+aa8ipJkj6wD5gkhIh5\n/fI6oBZgAwQCK95y/ChJkm5JknQrNDQ073eWC6Y6prQwa8HxF8cRQhAvUziadbUyQhHTMhWmURcN\nTBrgG+Orlmlla/PWPAx7mKVaVJFTRhdsMskGZL5DfAPjcsbMbDGTkMQQ7PfZM+vSLKKTo5luNx3X\nQa44tXGioUnRrz97RXkx5NgQLgYolFKXtFtSYFG994mwxDC+Pf0t8anxrO+6Psca2AAsynR/WAKX\nkFLSUlh+azm1DGsRmxLL34//Zqjl0LeW78yLI15HlNutqygMg4mOCeZ65qXSz5CnYRBCdBFCWOfw\nOAQES5JkDvD6b0hOfUiSpI3CKPwthNifqe9gIUSaEEIObABavGUc64UQtkII24oVc1++yA89avbA\nP9afm0E3lbMCuZAr92u81ogvTDRNblgaWyIQaglbbWXeCrmQcyPohhpGpgJ912Zs33aGV1kjMORC\nzqWXlxjvOp6JZzMMh6mOKYf7Hmao5dAsS3hFyUmfk3xx7AtiU2LZ2H0jXzb8Um2Z0v9FYlJiGHtm\nLCEJIaztvJb6xvVzbph59vhjyUzw+ufxP/jH+lO3Ql3WuK+hR80eTLWdWujPPz41Hlc/V0CxJJ3u\nUwTFSkG6RltpQtWlpMNAet07R+DQmw0kxX97E/BYCPHrG/sy54z3A7IuQr8jult0p4peFRZdX4R4\nPcnJXIlMW1I4ndOd0OogPbzyzXX2wtCkYhN0tHS49qoEhP9lviNc3x6S44hOjmarx1Z6HejF2DNj\neRD2gJGNRnJ6wGm+s/mOsMQwtnlsK5bhJsmSWHpjKVPPT6VehXrs7r37PyF69i5JlCXyvev3PI96\nzm8dfsvdMZvZKDgeAc2SJ6wQnhjOX/f/AuCM7xnaVGnDwrYLVQpuOOVzikRZIqC4acu80mCuZ56l\naE9pQdVPbgmwW5KkbwBfYBCAJElVgI1CiB5AW2Ao8ECSpPRbylmvI5B+kSTJBsUSlA8wWsXx5Atd\nbV3mtJrDONdxOHs4A2RRP013OquzbKWpjinmeuZqMQzamtrYmdlx5dUVhBDFf6f7WkvpURlt/tnQ\niBNGJiSnJdOsUjPG24yna42uSjmB0Y1H8yzyGb/e/pX6xvWV0+6i4HH4Y/538X94RXvxZcMvmdJ8\nSr5kDt5nUtNSmXxuMndD7vJL+19oW7Vtzg0zGwWrflCz4A7comD13dXEpSqSLhsaN8y31MXbOOSV\ncT/85ve5sl5l4lLjiE+NL1W+K5UMgxAiHOicw+uvgB6vty8BOV65hBDZ6+YVEe0+akePmj2UTujY\nlFilAzrdMKgqlf0m1qbWagsz/aTqJ1wIuMCLmBfUMlRNnE8VZHIZZ/3PsqNlX+6E3EFHLqdPZBiD\nvzyZ43KDJEksaLsArygvZl6cye5eu9+5hLVMLmPzw82sc1+HcTlj/uryF22qtnmn5/wvkCZPY/al\n2Vx6eYm5redib5GLquybwQcDnd/52ArDk4gn7Hu2D4AaBjXUInMSEBvA7eDblC9TntiUWNpUyfq9\nqqRbCVBI+xfn77SgvFeZz28yo8UM5bZ/bIauT7plT8+AVheNTBsREBdAZJLqBdDbV1OURzznf07l\nvgpDdHI0zg+d6bG/B5PPTSY4IZipTb7jjP9L5oZHUn9Vi6waOZnQ1dbl1w6/kihLZPqF6Wo3wJnx\ni/Fj+InhrL67mi41urDfYf8Ho5APhBD8fONnXHxcmNRsEgPrDcy54ZtGoQQ6m0HxfqacmwJAWc2y\napM5Ofj8IBISulq6NDRumC1Kq7Ku4qYnJCFH92uJ5b02DMbljPnO5jsAlt5YqnzdoKzCIZpZU0kd\nWJtaA+rxM5jpmdHQuGGRGwbvaG8WXltI171dWXF7BVX1q/J7h9851u8YjjZjMJiUKWb7JyPIxYFf\ny6gWTq2duBNyh1V3Vql9nDK5jO2PtjPgyAC8o71Z2m4py9ovK5GqtCWRP+//yS7PXYywGsE3jb7J\nuVEpMQoAB54fwC/WD4AdPXaopVZ3qjyVfc/20cC4AcEJwTnWdU83DKVNTO+9NgyAskSfV7QXZ3wV\nCSo5ie2pAysTKzQkDbUYBoCO1TriHuL+zktqpkcXjTkzBoeDDux/tp9uNbqxp/cetthvoXONzhkO\nN4MqMPVZxsHzjSEu5/DiHrV6MLj+YJw9nHH1dVXbeD3CPRhybAi/3PyFZpWbsb/PfnrUeqdqK/8p\nDj0/xFr3tfSp3Ycfmv+Qc6NSZBRiUmKYd2UeAH91/YsGxg3U0q+bnxthiWHKi3+X6l2ytUlfSvow\nYyhlaGloKSW3p1+YzrXAaxkzhhT1ftl1tXWpZVhLbX6GDtU6IBBcCHg3Co4JqQnserILh4MOjD0z\nFs8IT76z+Y7TA06z8OOFuf/A9CvBrFcZz5fXgQd7c2w63W46ViZWzLk8R2WZ7riUOJbcWMKQY0MI\nTQxlWftlrOu8rkBCaO87V15dwemKEy3NW+LU2innwIZSZBTS5Gm0/VfhMB9Qb0A2H4Aq7PbcTVX9\nqiSmJVLDoEaOulrltMqhpaGl9mXpd817bxgAOldX+M9NdUyZ6DYRzwhPDMsaEppQ+ES63LA2teZh\n2EO1lL9sYNyAyrqVlTHU6iIkIYRfb/9Kl71dWHh9IXraeiz+eDGn+p9iTJMxmOiY5N1JGT2Yl0lN\ndt83sKxu9maaZVjRYQUakgZTzk8hJS137aXcEEJwxvcMDocc+OfxPwysN5DDfQ9jb2Ff/BFbpQjP\nCE8mn5tMTaOaOUfryOVZjUKZ8iXaKAgh+OFcxoxnXut5auvbO8qbG0E36G7RndtBt+lUvVPu3zVB\nkWh9qZPSNdp3RHoI3tfWX1OhXAXGnhlLaloqL+Neqv1cjUwbEZkcSUBsgMp9SZJEN4tuXH55WVk1\nShV8on1wuuKE/T57tnpspbV5a7Z/up1/e/5L79q9Cx7WJ0lZLxzxITnKZ1TVr8rCtgt5HPGYP+7m\nT4k1Ha8oL8aeGcsP537AqKwRO3rsYE6rOWopsvQ+ERQfxDjXcehp67G289rs/z+PAzA/k2JNr99h\nlurf4XfJ+vvrOet/FoDjn6lXn3P3091oa2hjWNYQmZDluIyUjhx5rvtKKiUvA6UYsKlog66WLo/C\nH7G+63qGuQwjQZbAlVdX1H6uJhWbAOAe6q4Wnf8eNXuw/dF2XH1d6Ve3X6H68AjzYNPDTZzxPUMZ\nzTJ8VvczHK0c1VcRLXPNaFBs/y8AymZcfDpW78igeoPY4rGFNlXb0Mq81Vu7jEqKYu29tez23I2u\nti7T7abzeYPPP5TeLASxKbGMcx1HfGo8W+23Zl96e9OYz/ABnXcua6YS+57uU8q9j2w0Uq3V/WJT\nYjn4/CDdLLpx6eUlahjUoJFpo1zbl4hcowLyYcaAImHMvqY9x18cR7+MPn91/Uu5T93GoY5RHfS1\n9dVWwMPKxIpq5atlkRLPD0IIrgdeZ+SpkXx+7HOuBV5jZKORnOx/kjmt5qi9TCZO0dB5bsbznz+C\nlVkzaKfaTaWmYU1mX5yda1GjVHkqfz/+m54HerLLcxcD6g3gWL9jDLUc+sEoFAKZXMbU81N5EfWC\nXzv8mjX3RJ6Wsz+hhBuFc/7n+OnqT4Ai8vDbRt+qtf+9T/cSnxpPl+pduBl0k961er/1wi8QSDmn\ncpVYPhiG1zhaOpKclszOJzupb1xf+WUafXo0uz13q+08mhqaNK7YmLuh6qnCJkkS9hb2XA+6Tlhi\nWJ7thRBcC7zG8BPDGXlqJN5R3kxpPoVT/U8xodmE/PkPCku7KTA3UwRV5AvFhed1SKuOlg5L2y0l\nIjkCp6tOWfwwQgjO+5+n/+H+LLmxBEsTS/b23sucVnOy1NL4QMH47fZvXHl1hTmt5mR1zG7qrogo\nS6fGxyXan5COe4g7085PU0rdTLebrtZa3alpqex4vIOWZi3xivICoHft3nke92HGUEqpZVSLDh91\n4N8n/5IoS6S7RXflvgXXFrD0xlK1SWTYVLLheeRztfgFQLGcJBdyTvmcyrWNEIIrr67geMKRb099\nS0BcALNbzsalvwvDrYejX0Y9ZUzzREMz+wVmvjH82Q6AhiYNmdh0Iq5+rux/ptBbvBtyl+EnhjPe\nbTxyIWd1p9Ws77qeuhWyO7M/kH8OPT/EtkfbGNJgCP3r9Ve8mBKvMNb+mXS4ZvrDiNwLLZUUvKO8\nGe82XmkImlZqSo+a6g1TPv7iOCEJIQyzGsYR7yPYmdm9taBTujhnaZsxfPAxZGK49XCGnxjO5oeb\nGd14NDpaOvSp3QdtDW12PN6BT4wPv3zyi8qOzaaVmiIQPAh9kLv2TAGoU6EOdSvU5diLYwxpOCTL\nPiEEV19dZe29tdwLvUdl3crMaTmHfnX7FWndg2w4RUN8GCx7HeIXdF9xQZp4j2FWw7j86jJOV51w\n9nDGJ8YHUx1Tfmz1I/3q9vuwZKQG7oXe46erP9HSrCVT7aYqXsyprkYpmCWAIoFszJkxaElaNK7Y\nmHP+5/hfi/+p9U5dCIGzhzN1jOpgUMYA3xhfZR5UbqTP4ktb4acPM4ZMNK/cnJ61erLx/ka8oryw\nNLHkcfhjZrSYwY+tfuTaq2t8cewL7ofeV+k8jUwboSFpcDdEPctJAA61Hbgfep/nkRk1me+F3uPr\nk18z+sxoghOC+bHVjxz/7DiDGwwuXqOQjp5p9gvPyiYELTJVVvbwifHhO5vvONbvGIPqD/pgFNRA\ncHwwk85OorJuZZa3X472gbHZjcLsoFJjFGJSYhjrOpaYlBim2U3jYsBF+tfrr/YaH5dfXeZ51HOG\nWw3n4PODlNMsR9caXd96THr0oToyrYuSD4bhDWbazcSwrCFzLs9RGIaIxySkJjCo/iA2dNtAcloy\nw1yGscZ9TaE1fvS09ahfoT7uoepxQINinVNLQ4t9z/bhHeXNpLOT+Or4V3hHezOr5SzlhbVEGIQ3\ncYqGuZEEaWqy0KQCvT6qwp1XVzGTKZbuymiWUes68ftMkiyJSWcnkZCawKqaAzBaUgMe7Mlo0PQr\nxeehrVN8gywAyWnJTHSbyIvoF/zW4TcOex1GR1uH75t+r9bzCCHYcH8DlXQq0bZqW2XlwbwUUwPi\nXhsG/Q+GoVRjVM6IH1v9yJOIJ3iEeZAqT+XSy0sA2JrZsq/PPnrU7MGf9/5k6PGhvIh+Uajz2FSy\n4X7ofbX5LYzLGWNtYs2OxztwOOTAtcBrjLcZj8tnLnzR4IuSaRBeE5IQwuKbS+hhYcE+QyMcYuM4\nFvCKU/6v6BKfwJqbvyprdH+g8Agh+OnqTzwMf8jPL32pe3hy1gZO0eCwpngGVwhkchkzLszgVvAt\nFn+8mERZIldeXeE7m+/UvnRzNfAqd0LuMLLxSA57HSYpLSnbsm1OBMQGICG91Q9REvlgGHKgc43O\nONR24E7IHQClhhIoKjQtbreYFe1XEBAXwKAjg/jn8T8FzmS2qWhDoiwRz0hPlcebkJrAyjsrlTMQ\nk3ImuHzmwugmo0v0nXZoQihLbizh032fssdzD31q9+HoZ8eY970PZh1/RAJmh0WgK+TM2WWPzMkw\nV8XWD+TNv0dHctT7KN9FRtEpITFjx7yoUrNslI5cyJl3ZR6ufq7MbDGTTtU78cvNX6hjVIdB9Qep\n9VxCCNa6r6WybmX61unLzic7sTOzo16FenkeGxAbQGW9yiX6xiwnPhiGXJjXeh4tzBSVRl18XEhO\nS86yv5tFNw70OUBzs+b8fONnRp0ehW+Mb777T68adivoVqHHKITgiNcReh3oxcYHG+lZqyeakia1\njGqV6BDOoPgglt5Yyqf7P2Xnk530rNWTI/2O4NTGiar6VRWNPv4BnKIxbTKEWeGRPChXlm2G5RWK\nrU6GEPFhBpFvnAy5/3NFloVfp31CIqOiXkfDzY1UGIRSFkophGDZzWUc9jrMOJtxfNnwS7Z5bONl\n3EtmtJihdj/U5VeXuRd6j1GNR3Hl5RUC4wMZ0iDv2QIolpLUnhNUBHwwDLmgranNbx1/Uz7f9GBT\ntjYVdSuyrvM6fmz1Iw/CHtDvUD9W3VlFQmpCnv1X1qtMDYMahTYMHmEeDHUZyqxLs6isW5kdPXaw\npN0SvrP5jptBN/GJ9ilUv+8S/xh/nK448en+T/n3yb/YW9hzpO8R5redn7tzzmEN9lNf0aV8bdYY\nGeGt/TqQblVThYH4pfQUPylSIn0U/x8nQ6I0NJhayZRKsjQWhYaj4RStMAgapfPn/+e9P9nxeAdf\nNfyKMY3HEBQfxIYHG+hSvUueGfMFRQjBmrtrqKJXhX51+vHPk38w1zOnQ7UO+TrWN8a31PkX4INh\neCsGZQw40f8EAOvurctRLluSJAbVH8TRfkext7Bnw4MNOBxy4LTv6TyXl+zM7LgdfJu0XGoW5ER4\nYjhzL8/li2NfEBAbwPw28/m7599KqY1+dfuhpaHF34//LsA7fbc8j3zOzIsz6XWwF0e8jtC/bn+O\nfXaMhR8vzJcsiCRJzP50I7o6FZjTqBNZvDIJ4coLYG4Kru8NaakZ/4uViu+DHPhfRRPCNLX4te9e\nDOeqXiSqONnxaAdr763FobYD0+ymIUkSv93+DbmQZ4TdqpELARd4GP6Q0U1G4x2tEM4bXH+wssrj\n2/CM9CQiKaJU1hT/YBjyoKp+Vb5s+CUAXxz7IleJDFMdUxa3W8xW+60YlDFg8rnJjD49+q3OabvK\ndsSmxvIk8kme4xBCcOj5Ifoc7MMRryM4WjlytN9R+tXtl0W50VTHlJ41e3LI65Da60kUlAehD5h0\ndhL9DvfDzc+NYZbDONH/BHNazclYMsonpjqmzGo5iweRT9gxYGXOa+L7vsm4MF4tPU5UlUhJyHjP\nC0yz7d7UYw6XdHWY3mo2VqZWxTBA9XHw+UGW3lxKl+pdcGrjhIakwZ3gOxx/cZzhVsML/J3KizR5\nGqvuruIj/Y/oXbs3Gx9sRFdLlwH1BuTr+HQ5fHXkKhU1HwxDPpjQdIJy+zvX7zjx4kSubZtVbsau\nXruY2WImD8Me8tnhz1h2c1mO2j92ZnZA3n6Gl3EvGXNmDHMuz6G2UW329dnHFNspuWYrD7MaRqIs\nUa1SHvlFLuRcCLjAiBMjGHJ8CDeCbjCmyRhO9T/FFNspVNStWOi+7S3s6VCtA2vc1yjiw9OXRP6X\ng8rnyVkZF8xMshv/Ce5sz3hfi82z77f7FpyiuTH6NH882cGnNT9lcP3BRT9ONeLq68q8K/NoZd6K\npZ8sRUtDizR5Gj/f+BkzPbPcq8ypwMHnB3ka+ZSJzSfiF+PHSZ+TDGk4JN9VAC8GXMTKxApTnewG\nu6QjqVIXQJIkY2AXYAH4AIOEENnmqpIk+QCxQBogE0LYFuT4N7G1tRW3bhXeaVsY1rmvY+29tZTR\nKEOqPJWJzSbytfXXb82sDEsMY9WdVRzyOoSOlg6OVo4MsxyWJfa594HeVDeozprO2e9w0+Rp/Pvk\nX1bdXYWExKTmkxhcf3C+tN3HnB6DZ6QnJ/ufLJKIiNS0VI6/OI6zhzPPo55jpmfGMMthfFb3szxj\nvQtCUHwQDgcdaFq5Kes6r8v+/48LgeX5kMqY+hz0C2+kigwh4PD3cHf729s1GgT9NyifhiSEMPDI\nQIzKGvFvz39LdHRaXlx9dZXvXL+joUlDNnTdoHwve57uYf7V+Sz7ZBn2Ne3Ves741Hh67u9JdYPq\nbLXfysyLMznrf5aT/U/mK7AjKimK9rvbM7rxaMbZjFPr2FRBkqTb6dfft6GqJMZMwFUIsUSSpJmv\nn8/IpW1HIcSbKm8FOb5Y+cryK/Y+20s5zXLUMarD73d+537ofRZ+vDBXiQxTHVPmt52Po5Ujq++u\nZq37WnY+2cnIRiMZVH8QZTXLYmdmh8sLF2RyWZZ1S59oH2Zfns390Pt8XPVj5raai7l+DneHuTDM\nahijT4/mmPexQstx54fYlFj2Pd3H9sfbCUkIoW6Fuiz+eDH2Ne3fSZaymZ4ZE5pNYMmNJbi8cMle\nslO/UsYykxCwuCrkVD1reZ3sr410hY/y/M28O4SAk7PhWj6Xwb4+BdVbZns5TZ7GzIszSZQlsrn7\n5lJtFO6F3mPi2YlYGFqwtvNa5XuJTo5m1Z1VNK/cPIuumbrY+GAj4UnhrO60Gp8YH074nMDRyjHf\n0X6XX11GLuS0q9pO7WMrClSdMXgCHYQQgZIkmQPnhBD1c2jnA9i+aRjye/ybFMeMAeCs31kmnJ3A\ndzbfoaetx6+3fqWKfpXscsW58CD0ASvvruR64HXM9MwY12QcWhpazLo0i509dyrXgI94HWHBtQWU\n0SzDzBYz6VmzZ4E1X4QQDDgyALmQs7/PfrWrO/rH+vP347858OwACbIEWpq1ZIT1CNpUafPOlSTT\n5Gl8dfwrXsW/4nDfw/me2iNLhoWVCn/iXr9B48+hTCEvtAkRcGoOuBcyMGDQNrB0yLPZ+vvrWX13\nNQvaLqBvnb6FO1cJ4GnkU4afGI5RWSO2fboty5LMz9d/ZqfnTnb32p2v315BeBn3kj4H+tDVoitL\n2i1h1sVZnPE7g8tnLvlWH55xYQbXAq9xdtDZElW9Lb8zBlUNQ5QQwuj1tgREpj9/o90LIBrFUtJf\nQoj1BTn+TYrLMABMPT8VNz839vbeS1RyFFPPTyU2JZbZrWbjUNshXxfFa4HXWHl7JQ/DH6KnrUd8\najzfN/2erxp+xaLrizjsdZhmlZqx9JOlKtUrPux1mNmXZrO60+p8hdflhRCCOyF32P5oO25+bmhK\nmtjXtGeo5VAsTSxV7r8geEZ4MvjoYPrU7sP8tvML35H3OdiW98W2yLF0gIFbC5xjcC/0Ho4ujnSr\n0Y2lnywtdXLP6XhHe/P1ia/RlDTZ1mNbFsfys8hnDDwykAH1BjCn1Ry1n3va+Wmc8z/HkX5HSE5L\nps/BPgxtODTfUU8xKTF039udztU7s/DjhWofnyqozTBIknQGyOnqNBvYmvlCLklSpBAi21xLkqSq\nQoiXkiRVAk4D3wshLmQ2DG87/vW+UcAogOrVqzf39c1/Mpk6CUsMo++hvlTUqci2T7eRnJbM9AvT\nuRl0ky7Vu/Bj6x/zlY4vhMDNz42/7v/F44jHWfaNaTKG0Y1H5ysk7m2kylNxOOiAnrYeu3rtKvSd\nS2paKid9T7L90XYehT/CsKwhg+oN4vMGn1NJV4U7cBX59favbHm4hc3dNysd+WpDlgy7hsKzk+rt\nNzMaWjD6AlRWT7RQbEosA48MBGBP7z2ltrypb4wvI06MIE2ksaX7FmoZZeSqCCH49tS3PI54zLF+\nxzAql+d9ZIG4HXyb4SeGM7rxaMY3Hc/U81M5738el/4u+XYi/3nvT9a4r2FP7z00MG6g1vGpSn4N\nA0KIQj8AT8D89bY54JmPY5yAqYU9XghB8+bNRXFy9dVVYbPVRow8OVKkpKUIWZpMbH6wWTTd1lR8\nsvMT4errmu++5HK5sHa2zvJY575ORCVFqWWsh58fFtbO1uLki5MFPjY4Plj8cfcP0X5ne2HtbC16\n7e8ldj3ZJRJSE9QyNlVJSE0Q3fd2F7329xJJsqTiHk6xIpfLxfTz00WTrU3E3eC7xT2cQuMX4yc6\n7+4s2v3bTjyNeJpt/2mf08La2Vr88/gftZ87WZYseh/oLbrt6SbiU+LFraBbwtrZWqy9uzbffcQm\nx4o2/7QR413Hq3186gC4JfJxjVV18esw4Ph62xE49GYDSZL0JEkqn74NdAMe5vf4kkgr81bMbT2X\na4HXWHB1ARqSBiOsR7Cz104q6VZi4tmJzLk0h9iU2Lf2I4Rg/f31yud96/Sl/UftWeO+hm57u/Hr\nrV8Jig9Saaw9avagpmFN1rqvzVcinRCCuyF3mXZ+Gt33dueve39hZWrFui7rONT3EIPqD0JHq2Qo\nb+po6TC31Vx8YnxyzEx/nzjifYTjL44zpskYbCrZ5H1ACeRl3Eu+OfkNSWlJbOi2IVshpiRZEstu\nLqNuhboMrDdQ7eff9GATL6JfMKfVHMpplWPpjaVU1q3McOvh+e5jp+dOYlJiGNN4jNr0fowGAAAg\nAElEQVTHV6Tkx3rk9gBMAFfgGXAGMH79ehXg+OvtWsC91w8PYHZex+f1KO4ZQzqr76wW1s7W4o+7\nfwi5XC6EECJFliJW3l4pGm9tLDrt7iTO+JxR7stMalqqmHd5nrB2thZTz00VzbY1E05XnIQQQjwJ\nfyKmnZ8mGm9tLJpsbSImn50s7gTfybGf/HDixQlh7WwtjngdybVNfEq82Pd0nxhweICwdrYWrf9u\nLZbeWCp8o30Ldc6iZNq5aaLZtmbCL9qvuIdSLPhG+4oWO1oIRxdHIUuTFfdwCkVgXKDovre7aP1P\na+ER5pFjm7Xua4W1s7W4EXhD7ef3ivQSTbc1FdPOTxNCCHHg2QFh7WwtjnodzXcf8Snxot2/7cSY\n02PUPj51QT5nDCoZhuJ6lBTDIJfLxeyLs4W1s7VYdG1Rlh/l/ZD7ov+h/sLa2VqMdx0vAuMClfvi\nU+LF2NNjhbWztVh5e6WQy+ViottE0Xl35ywX/4DYALH85nLR+p/WwtrZWgw6Mkgcen5IJMuSCzTO\nNHma+OzQZ6LHvh4iJS0lyz7PCE+x8OpC0ervVsLa2Vr0PdhX7HqyS8SnxBfyv1L0BMUFiRY7Woix\np8cW2niWVlJkKWLwkcGizT9tsnzHShOBcYHi032filZ/txIPQh/k2OZV7Cthu91WTD47We3nT5On\niWHHh4k2/7QRoQmhIi4lTnTY1UEMOTakQN8n54fOwtrZukQv5X0wDEVEmjxNLLuxTFg7W4sfzv6Q\nZa07JS1FbHmwRdjtsBN2O+zENo9tIiE1QTi6OIrGWxuLXU92Kdvu9dwrrJ2tc1xXjU+JF7ue7BJ9\nDvQR1s7Wov3O9mLN3TUiJD4k3+N083UT1s7WYq/nXpGYmigOPT8kvjr2lbB2thbNtjUTMy/MFLeD\nbpfaC2v6j/KM75niHkqR8vvt34W1s7U47XO6uIdSKPxj/BUzhb9bi3sh93JtN+XcFGG73Va8jH2p\n9jHs9twtrJ2txf6n+4UQQqy8vVJYO1u/dTxvEpscK9rvbC++Pfmt2senTvJrGFQKVy0uijNcNTe2\nemxl+a3lNK/cnJUdV2aJrX8Z95JF1xZx8eVF5WtL2i2hZ62eyufB8cF02duFH5r/wNfWX+d4DiEE\nVwOv8vfjv7kQcAEtSYv21dozoN4AWpu3RlNDM9fxCSGw3WFLijwFLUkLmZBhYWDBgHoDcKjtoPbo\njqImVZ7KoCODiE+N51DfQyXGD/IucQ9xx/GEI31q92FB2wXFPZwC4xfjxzenviEhNYH13dZjZZJz\ndNbNoJt8ffJrxjUZx1ibsWodQ0hCCH0P9qWBSQM2dduEf6w//Q71o5tFN35u93O++hBCMP3CdE77\nnmb7p9tpVLGRWseoTvIblVRyMi9KOY5Wjixtt5R7ofcYfHQw90LvKfdV1a/Kms5rsDaxVr528eVF\nguODlc8r61WmXoV6XAy4SG5IkkSbKm1Y03kNR/sdZajlUO4E32HsmbH02K+oKpe5T4DIpEh2PNrB\nwCMDSZGnACATMjZ338zhvodxtHIs9UYBQFtDm9ktZxMYH8iG+xvyPqCUk5CawKxLszDXM2eGXYkU\nC3gr3tHeDD8xnGRZMpu7b87VKMjkMpbcWEIVvSqMsB6h1jHIhZzZl2YjEzLmtZ6HQDD3ylzKapZl\nUrNJ+e5nt+duTvicYHzT8SXaKBSED4ZBjfSo1YMt3bcghMDRxZGNDzYqI4HOB5zHI9yDTz76hG8b\nfctpn9P0PqhQbEwvAtSuajvcQ9zzjGYCqGFQg8m2k3Ed6Mry9ssVekvua+i2rxtjz4xl4bWFTHSb\nSKc9nVh6cymaGprMajmLjtU6oqWhRUWdiqU2+Sk3bM1s6V2rN1s8thS65GppYfmt5QTEBrCg7YJc\nxRRLKs8inzHixAjkQs6m7pvemrm89+lenkY+ZardVMpplVPrOLY/2s61wGtMt5tODYMa7Hyyk9vB\nt5lmN43KepXz1cej8EcsvbmUdlXb5TrTL5XkZ72ppD1Kko8hJ6KTo8XUc1OFtbO1+ObEN8qIi/6H\n+ovE1EQhhCJee6LbRGHtbC3s99qLM75nxO2g28La2Voc8zpW4HOmydPE/qf7s+VEvBlZEZoQKlr9\n3UqMOT2m1PoT3kb6+/v25Lf/yfcnhBAX/C8Ia2drsezGsuIeSoF5FPZIfPzvx6Ljro7CK8rrrW0j\nEyNF23/biq9PfK32z/Jx+GNhs81GTHSbKORyufCL8RN2O+zE6FOj832umOQYYb/XXnTe3VlEJEao\ndXzvCoooj+EDOWBQxoBfPvmF+W3mcz/sPl33duVl3EtGWI9Q3vVUK1+N3zv+zvqu6xVT17OT+P3O\n7wCc8j2Vr/MIIXgY9pBlN5fRdW9X5l6Zi46WDl1rdMWhtgPtqrZDS9Ji5sWZDDwykO2PFAqdY5qM\n4dLLS0q9+P8SpjqmjG86nquBV/P9fyxNRCVFMffKXOoY1eH7Zt8X93AKxM2gm4w4qfgNONs7U8vw\n7dX3/nD/g7iUOGa0mKHW2W2iLJHpF6ZjXNYYp9ZOCATzrsxDQ9LAqY1Tvs4lhOKYwPhAlrdfXqJL\n6RYGVdVVP5ALkiTRr24/bCrZ0OdgHwC2PdpGHaM6WabOrau0Zm+fvex/tp817gpVTVc/VzwjPHOc\nYqempXIr+BYXAi5wzv8cAXEBaGto83HVj5lqO5X2H7XPoqYZmRSJywsXDnsd5pebv7Di1gplLev5\nV+fjUsWl1BUqz4vB9Qdz4NkBlt9azicfffKfcUQLIVhwbQFRyVGs7byWsppli3tI+cbNz41p56fx\nUfmP+KvrX3lqgD2NfMqep3sYXH8w9SrUU+tYVtxa8f/2zjysqmpt4L/FKCKIgKKCE04hOOQ84yyi\n4nCzTExtMLt1uw1mefNalnVvn90Grexa5pB6M3NE0UwrUUFxwAGcBVE4MiMgHDicYX1/ACcIhAMc\nBnX/nmc/Z++111r73Wvvs969pvflRuYNvhn9DU4NnPjx8o+cTDzJkgFLTLZNtvHSRg7cPMDrvV6/\nbxcUlocyK6kWGPXTKJLUSTjZOnE3/y6BXoG82OPFUn4KcrQ5vPzby5xMPAnA7C6zmdttLjqDjiOq\nIxyOP0zY7TBytDnYWtrSt3lfRrcZzcg2I3G0caxQjuiMaHZH72Z3zG6S1cnG8C9HfMnAlgOxtjS/\nmey64lTiKZ7e/3SNzGSpK4Jjgll4ZCF/f/TvzO02t67FMZmd13fybti7eLt4s3LkygonO0hZYA/p\n8p3LBE8JNt16rgkcijvEy7+9zBzvOczvPR9Vtoopu6bQo2kPVo1eZVJrYW3UWj49/SnDWw3n8+Gf\n1yvrqRVRK9ZV64r7TTGsiFjBt5HfsnrMavbd2Me2a9to1rAZLz/6MhM9J5aYZqoz6Hh0w6Nl5tOs\nYTN8PXzx9fClb4u+Vf4S1hv0nEw6ydxf/qhcHG0cGd1mNH7t/Ojj1qfcqa/3C0UG0IImB1XKl0V9\nJDEnkalBU/Fs7Mk6v3XVNrBYWxRN4x7QYgCfD//cJN8Qv976lVd/f5V/9P0HM7xmmE2WW1m3mB48\nHY9GHmz03wjAnJ/nEJMZw/aA7bRs1LLc9AZp4LPTn7Huwjr82vrx4eAP77vWtqIY6hFZ+VmM2zaO\nXF0uXV27Ym1pTXhCuPF8W8e2dG/anUR1IhdSL5CtzS4zn0X9FvGXjn8x25d9el46E7ZP4K72Ln5t\n/Tgcfxi1To1LAxdGtxnNmLZj6Nms532rJG5n3yZgZwDDWw3nY9+P61qcKiOl5MVfX+RU4im2Bmyl\njWObuhapQqSULI9YzndR3zGmTcGaAFMq0Xx9PpN3TcbGwoatAVvNpgBztDkEBgeSlpfGD+N/wMPB\ngw+Pf8jmK5v5dNinjG4zutz0WoOWJWFLCIoO4slHnmRh34X3VUuhCGUdQz3C0caRNWPXEOgViNag\nLeXjOTYrll3RuwhPCMe/nT/PdX0OgFd7vkrk7EjW+62nZ7OefBj+IQE7A9gTsweDNFRbLucGzrw3\n6D0AOjh1IOSJED4d9ik93Xqy4/oOntn/DCN+GsGSsCWEqkLR6rXVvmZt0rJRS57xeYafY3/mdNLp\nuhanyuyO2c1R1VFe6fnKfaEU8vX5LDq6iO+ivmNap2ksG7rM5C/rjZc2Enc3jjf7vmk2pWCQBt4+\n8jaxWbH8x/c/eDh4sCdmD5uvbGZ2l9kVKoVcXS6v/v4qQdFBvNTjJf7R9x/3pVKoDEqLoQ5Qa9XE\nZsXiaOOIg40D+2P3899z/yUlN4Uh7kOY130en5z6hDt5dwiaHIQQAiklR1VHWR6xnCt3rtCxSUde\n6vESI1qNqPaMjTdD3uTArQNsHr/ZOOCt1qo5ojrCwZsHjS0JBxsHhrcazqjWoxjoPvC+GPzM1eUS\nsDMAJ1snNo/ffN+1flLUKUzaNYkOTh1Y57eu3ldImZpMXv39VU4lneJvPf7G892eN/n9TM1NZfz2\n8fRt3pcvRn5hNpmK/LW/1ectZnaZybU71wjcG0gXly6sHrO6XAWUqcnkb7/+jXMp5/hn/3/yeOfH\nzSZXXaB0Jd1n5Opy2XRpE+surCNTk2kMX++3np5uPY3HBmlgf+x+vjr7FTezbuLl7MWLPV7E18O3\nygriTt4dJu+aTLOGzfjf+P+V8tWs0Ws4dvsYB24e4FDcIbLys7CzsmNgy4H4evgy1GOoyS4P64Kf\nb/zMgsMLeHfAuzzW6bG6FsdkpJS88vsrhN0OY+vErbRt3LauRSqXuLtxvHjwRVTZKpYOWlrC5Isp\nvBP6DrtjdrNz0k6ztYyKxisC2gfwwaAPyNHm8GTwk2Rrs9kyYQtNGza9Z9pTiaeMU1I/GvIRY9qO\nMYtMdUmtOOqpq62+L3CrDjn5OXJt5FrZb1M/4wK1w3GHSy260eq1ctf1XdJvq5/0Wecjn9j9hAyJ\nC6nyQqCDsQdNckqSr8+XofGhcumxpXLklpHSZ52P7Lquq5wRPEN+c+4beTX9ar1bWGYwGOSsvbPk\n0M1DZaYms67FMZng6GDps85Hro1cW9eiVMjZ5LNy6OahctAPg+TJhJOVTn8h9YLsuq6rWRftXUu/\nJvtu7Cuf3POkzNPlSYPBIF/7/TXZfX33cmXMzs+WS48tlT7rfOTYrWPlqcRTZpOprkExond/k6fL\nY8SWEdzVFpjH8HL2Yrb3bMa0HVPii15r0LIneg+rzq9Cla2im2s3XuzxIgNbDqx0C2LhkYXsv7Gf\nNX5reLRZ2TOjiiOl5HL6ZQ7FHyIkrsDkBxTYhvL18MW3lS993PrUi2mwl9Iu8cSeJ3iqy1Ms6LOg\nrsWpkNTcVKbsmkIrh1ZsGLehXneB/RL7C28ffZtmDZuxcuTKSrdspJTM+XkOsVmx7JmyxywuSZPV\nyczaNwuNXsPm8Ztxs3czutx8o/cbzPaeXWa6I/FHeP/4+yTlJBHoFcjLj75s0kyq+wWlK+kBIC03\njZE/jUQv9bR1bEtsVizNGjYj0CuQv3T8S4n53Vq9lp3RO/nm/Dck5iTSzbUbz3d7nqEeQ01WEFn5\nWUzfMx2NTsOWiVsq3T2UrE4mJD6EkLgQjiccR6PXYG9tz8CWAxneajhD3IfUqcG+JWFL2HV9Fzsn\nm6+roqZ4/dDrHIo7xE8Tf6K9U/u6FqdMpJSsjlzNijMr6NG0BytGrKjSCmBzd/VlajKZ8/Mcbmff\nLjDQ5+rNT1d/4v1j7zPRcyIfDv6w1H8iIy+DZSeXsTtmN56NPXl/0Pt0b9q92rLUNxTF8IDw7/B/\ns+XKFoKnBnM94zrfX/ye8IRw7KzsmNxhMjO9ZtLasbUxfr4+n13Ru/gu8jtU2SoecX6E57s9z8jW\nI00auLySfoXAvYH0aNaDVaNWVflLNVeXS3hCOIfiDhESH0JqbioWwoIeTXvg26pgLYZnY89aNeRX\nNLg5sOVAPhv+Wa1dt7L8EvsL80Pm1+uFbGqtmn+G/pMDNw/g386f9we9X6XJCHm6PAJ2BuBo48iP\nE36sdstIrVXz/IHnuZh2ka9HfU2/Fv04ePMg80PmM6jlIJaPWF6ixS2l5Jebv/Cv8H+Rpcnima7P\nMK/bvPtufYKpKGMMDwi3796WPb7vId8+8rYx7HLaZfn2kbdlj+97yK7rusq/HfybPBp/VOoNemOc\nfH2+3HFthxy/fbzRM1twdLBJrh+LjPEtP73cLPegN+hlZEqk/CLiC6PrUJ91PnLUT6Pku6HvygOx\nB+RdzV2zXKsivj77tfRZ5yMjkiJq5XqVJT03XQ7dPFROC5pWyttefeFW5i05eedk2W19N7kual21\nxpSKnoc53HXm6/Ll8788L7ut72Z02HQi4YR89PtHZWBwoFRr1ca4eoNe7r+xX04LmiZ91vnIaUHT\n5OW0y9WWob6DMsbw4FC0cnrN2DX0ad7HGJ6iTuGHyz+w7do20vPSae3Qmsc7P87kDpON3Ux6g56f\nY3/m2/PfEp0ZTRvHNjzt/TQT208s96vo3bB3C+w3jfyKoR5DzXo/iTmJHFEdIVQVyvGE4+Roc7AS\nVnRv1p3B7oMZ1HIQnZ0718jUTLVWzcQdE2neqDkbx22sd6bHFx1dxN6YvWyesLlcc9R1xVHVUd48\n/CYWwoKPh37MgJYDqpxXYk4iATsDGOw+mE+HfVotufQGPW8deYv9sft5f+D7TOk4hUtpl3h6/9M0\nb9ic9ePW09i2MTqDjn039rE6cjUxmTG0cWzDsz7PMrH9xPtmNXl1ULqSHiBydblM2TUFW0tbtk7c\nWmowN1+fz4GbB/jxyo+cST6DraUt/u38eeKRJ4wOUAzSwK+3fuXb899yKf0STe2aMqvLLB7r9FiZ\n9vzzdHk8te8pVNkqtkzYgoeDR43cm9ag5VzyOUJvh3JUdZTL6ZcBcGngwiD3QQx2H8yAFgPMOjax\n49oO3gl7h//4/oexbceaLd/qcjzhOHN/mcvcrnP5e8+/17U4JZBS8l3Ud6yIWEGnJp34fPjn1X4n\nFh5ZyIHYAwRNCcK9kXu1ZFt6fCk/Xf3JOLAclxXHU/uewtrSmg3jNuDcwJmd13eyJmoNqmwVHZt0\nZG7XuYxpM6ZeD+ybm1pRDEIIZ+BHoC0QCzwupbzzpzidC+MU4Qm8I6X8XAixBJgLpBSee1tKubei\n6z5sigHgcPxhXvr1pQr7nS+nX+bHKz8SHBNMri4Xbxdvpnacin87fxrZNELKAvegayLXEJ4YjoON\nA9M7TyfQK7DUYHNcVhxP7HkCDwcP1o9bXytWSlPUKYTdDiNUFUpYQhiZmkwEgq6uXRnkPohB7oPw\ncfGp1p9Zb9Azbc80crW57Jq8q170J2v0GqbumgrAtoBtZndKUx1ytDm8G/Yu+2P349fWj/cGvlft\nmTrnUs4xc+/MaitBgzTw8cmP2XhpI891fY5Xer7C7ezbPLv/WbK12Xw18ivOJp9l/YX1JOcm0821\nG3O7za3Wup/7mdpSDMuAdCnlR0KIhUATKeU9/QwKISwBFdBPSnmzUDFkSyn/U5nrPoyKAWD+ofn8\neutXVo5cyUD3geXGzcrPYnf0brZe3cr1jOvYWdnh19aPqR2n0r1pd4QQRKVGsSZqDQdvHsTG0obJ\nHSYzu8tsWjm2Mubz+63feeX3VxjWahifDfusVr+u9AY9F9IuEKoK5ejto0SmRCKRNLZtzMAWA42K\nwtXOtdJ5h6pCeeHgCyzovYBZ3rNqQPrK8cWZL/jm/Dd8M/qbanXPmJuLaRdZELKA+Ox4Xu35KnO8\n51S7QjVIAzP3ziQxJ5E9U/ZUWcnoDLqCmWbRu5jpNZM3+7xJdEY0z/7yLOl56bS0b0lqbir5hnz6\nNu/L3G5z6de830OpEIqoLcVwBRgmpUwQQrQADkkp79kxKoQYA7wrpRxUeLwERTGYTI42h1n7ZqHK\nVrFh3AY6NulYYRopJZGpkWy7to19N/aRq8ulg1MHpnacykTPiTg1cOJG5g3WX1jPruhd6A16RrQe\nwWzv2fRo2gMhBJsubeKjEx/xROcnWNRvUZ39sTLyMjiWcIyjqqOEqkJJy0sD4BHnRxjUskBJ9GjW\no9TK7Xsx78A8olKj2Dt1r1lNO1eW6IxoHtv9GH5t/Ux2QF/TSCn53+X/8cmpT3Bu4Mz/Df0/ern1\nMkveu6N38/bRt/lw8IcEtA+oUh4avYY3Q97kt7jfeLH7i7zQ/QX+d/l/fHTiI2OcJrZN8Gvnx6T2\nk/B2Ldun9MNGbSmGDCmlU+G+AO4UHd8j/hogQkr5ZeHxEuBpIBM4Bcz/c1dUWTysigEKBuwCgwOx\ntLBkk/+mcpf0/5kcbQ77buxj+7XtRKZGYmVhxTCPYQS0D2Cwx2Ay8jL44fIP/HjlR7Lys+jq2pVZ\n3rMY1XoUK86sYG3U2nozhdIgDVy9c9WoJM4mn0Unddhb29O/Rf+C8YmWg8s1t30l/QrTdk9jVpdZ\nvNHnjVqU/g8M0sDTPz9NdGY0QZODcG7gXCdyFCcjL4PFYYs5FHeIYR7DWDpoqdnGeIoG/93s3djo\nv7FKEwxytDm88tsrhCeGM7vLbBxtHfnizB+2lXxcfJjXfR6D3AeZ/JHwsGA2xSCEOAiU5dZoEbC+\nuCIQQtyRUpa5wkUIYQPcBryllEmFYW5AKiCBpUALKWWZHrWFEM8DzwO0bt26182bNyu4tQeXi2kX\nmfPzHJo1bManwz6tkoerK+lX2BW9i+CYYNLz0nFu4Ix/O38mdZhEa4fWBEUHseHiBm7dvUVL+5bM\n8JrBqcRTHIo/xNJBS5ncYXIN3FnVuZt/lxMJJzh6+yhHVUdJzEkEwLOxp3EQu5dbr1Jz7ReHLiY4\nJpigyUE1NsBeHluvbuW9Y+8ZZ9LUNaeTTvPW4bdIy0tjfq/5BHoFmrWFWDTDbsO4DVXyfJaam8rw\nLcPveX735N313qZUXVLvupKEEJOAl6SUZVqiEkK0BfZIKX0quu7D3GIo4kzyGeYfms/d/Lu8M+Ad\nJrafWKV8tAYtoapQgqKDOBR3CK1BS6cmnZjUfhJ+7fyISo1i/YX1RCRHYGNhQ74hH4CvR33NYPfB\n5rwlsyGl5EbmjYLWxO1QTiWeIt+QTwPLBvRp3ofB7oMZ4jGEVg6tSMpJYvyO8YxpM4Z/DflXrcqZ\nmptKwM4AOjfpzJqxa+q071tv0LM6cjUrz63Eo5EHy3yXGWe0mYubWTeZsmsKY9uOrVSXmSpbRagq\nlO3XthvNrgD0dutNbFYsqbmp9G3el+XDl5c5w07hD2pLMXwMpBUbfHaWUr55j7ibgf1SyrXFwlpI\nKRMK91+jYFB6ekXXVRRDAam5qSwIWcCppFNM6zSN13q9Vi07Mxl5GeyL3UfQ9SCi0qKwEBb0a94P\nf09/Wti3YMf1HQTHBBvjv9jjReZ1m1fvTUGrtWpOJZ0qGMRWHeXW3VtAgYOkwe6DOZl4kit3rrBz\n0s5aNT/x5uE3OXjzIFsDtuLZ2LPWrvtnYjNjWRy6mLMpZ/Fv58/i/ovNXsFKKXnh4AucTznP7im7\ny50wkJabxvmU85xIPMFR1VFis2JLnJ/pNZN53eax6vwqNl7ayKjWo/ho6Ef3hRn4uqa2FIMLsAVo\nDdykYLpquhCiJbBaSulfGM8euAV4Sikzi6XfAPSgoCspFphXpCjKQ1EMf6Az6PjizBesiVqDg7UD\nT3o9yUyvmVWyWVOcmIwYgm8EszdmL/HZ8dhY2ODbypf+LfoTlRrFjus7jHHf6P1GiUV19Z2bWTc5\nqjrKEdURTiacNLaCABb3X8xg98EVunmsLmGqMOYdnMdfu/+VF3u8WKPXuhd6g56NlzbyxZkvsLW0\nZWHfhUzwnFAjLZeDNw/y2qHXWNh3IYFegcZwrV7L5fTLnE89z7mUc5xPOY8qWwWAraUtvd16k5yb\nzLU713Br6MbyEctxsnXizZA3OZ96nkCvQBb0XvBQrUWoDsoCt4eMi2kX+fb8txy8dRA7Kzse7/Q4\n0x+ZXu1+cykl51PPExwTzP7Y/aTnpeNg40AHpw6cST5jjGdnZcd4z/E83ulxvFy8qns7tUauLpeT\niSd56deXSoS3b9yeIR5DGOw+mJ7NeprVQqxWr2Vq0FQkku0B2+tkHcXNrJssDl3MmeQzDPMYxjsD\n3qnURIbKoNaqmbRrEvZW9nzs+zHRGdGcTz3P+ZTzXEq7ZFTMbg3d6Na0G91cu9GtaTc6NOnAZ6c/\nY+vVrfRr0Y9lQ5dxJvkMi0MXI6XkvYHvPRA+EmoTRTE8pFy/c53VUavZd2MfBmnAs7Envh6+DPEY\nUqmpnGWhM+gITwgnOCaYX2/9ilqnLnHeysIKnUGHt4s30zpNY1y7cfeNyeLs/Gz8tvvRyLoRMx6Z\nwRHVEU4nnUZr0NLQqiEDWg5gsPtgBrsPprl9WXMxTGdN1Bo+O/0ZK0euZIjHEDPdgWkYpIFNlzax\nImIF1pbW/KPvP8zeStAb9KiyVVzLuEZ0RnSJGUNF2Fra4u3iXaAImnajq2vXEuWamJPI64deJzI1\nkmd8nuGF7i+wImIFGy9tpItLF/4z9D8l1tsomIaiGB5yVNkqfrv1GyHxIZxOOo3OoMPB2oHezXvT\n2bkznZp0olOTTng08qhSMzxPl0eoKpRNlzdxMvFkmXHsre0Z3248j3V67L5oRRRV2EVe89RaNeEJ\n4RxRHeGo6igJOQW9nJ2adCoYwHYfQvdm3SulbJPVyUzcMdHs7itN4VbWLRaHLiYiOQJfD1/eGfAO\nzRo2q1JeeoOelNwU4u7GocpWocpWEXc3jpiMGGIyY9DoNaXSPO3zNB2dOtLBqQMdmnS4Z7mFJ4Sz\nIGQB+YZ8Phj0AZ2dO7MgZAEX0i4Q6BXI671erxer1e9HFMWgYCQ7P5vjCcc5HH+YM8lnuHX3FgZp\nAKCBZQM6OHWgXeN2NLdvbtzcGrrR3L45jjaOFX5NJuYkMnpr+Q7VfVx8eKzTYwa33voAABYXSURB\nVPi188Pe2t5s92ZOcnW5+G/3p41jG9aOXVvivqWURGdEG8cmIpIi0MkCZdu/ZX+GuA9hiMeQCldh\nF9kH2jlpZ6198Wr0GtZGrWV15GpsLG1Y2HchEz0nlvtcc7Q5pKhTSMlNITU3lYScBOLvxhuVgCpb\nhc6gM8YXCNzs3fBs7FlQ8Tt1oG3jtiw6uog8XR47J+/E0caxXDkN0sC6C+tYHrGcto5t+Wz4Z1y/\nc50lYUtAwNKBSxnZZqS5iuWhRFEMCvckV5dLTEYMV+9cNW637t4iRZ2CXupLxLWzsqOJbRMa2zbG\nydYJJ1snHG0djfv21vbYWdmhl3oWHlkIFMz2adKgSYkxiOJM9JxIQIcA+jbvW+9mNP1w+Qf+Ff4v\nVo1aVa7Zkez8bGNr4kj8EZJzk402nYr8TXRq0qlE5RuRFMHsn2fXqpG8kLgQPjrxEfHZ8fRy68Xz\n3Z7H1tKWTE0mmZpM7mjukKIuqPyLlECKOqVUNyGAk60T7o3ccW/kjoeDh/HXo5EHLexblBqH+S7y\nOz6P+JzPh31eYYUekxnDe2HvEZEcwZg2Y3iu63N8ceYLjqiO0NW1Kx/7flwtQ3sKBSiKQaHS6Aw6\n0nLTSFQnkpiTSFJOEknqJDI0GcYtU5NJhiaDLE0WEvO8Ox2bFHQv2FjYYGNZuFnYYG1pXSLM2sLa\neK7o2NLCEkthiZWFFVYWVlgKSywtLLESJY+tLayN+5bCskRaS2FprMC1ei0TdkygSYMm/DD+B5P6\n3qWUXL1z1eiUKDI1EoCW9i0Z6jGUYa2G0dOtJ7P2zSJDk8GuSbvKHHuRUqIz6NDoNeQb8snX56PR\na9DoNWj1WuN+ni4PtU5NjjaHXF0uOdoc1Fo1ObqCX7VWzZU7V4xdXxXR0KohTRs2xdXOlaZ2hb8N\nm/6xb9cUN3u3Sk2FjsmI4fE9jzPEfUi5TpG0ei1rotaw6vwq7KzseKnHSySpk9hwcQM2ljb8tftf\nmfHIjHrhHvZBQFEMCjWK3qAnW5ttrJxydbmotWoy8zN5/dDrxnjP+jyLhbAgR5vDicQTXM+4Xm6+\n1hbWNLBsYKwYzaV8KsJKWBkVRfGv5eb2zRGUVA7Fj8tSHGm5aeTp8+55LQthgaONI3qDHp3UYZAG\n435VsbOyo6FVQyyEBSm5KSXOPfnIk7jaudLYpjGNbUtuRa0+c5Kvz2dG8AyS1clsC9h2z9lOkSmR\nvHvsXa7ducbYtmPp3rQ76y6sI1mdTED7AF7t+WqNzZR6WDFVMTz4nikUagRLC0tj5fJnzs86z/cX\nv+ez05/xW9xvfD7881ILuGIyY/j91u/suL6Dm1l/mDfRGrRoDVre7vc2k9pPwtrSGq1eS74+36gs\n8g35aPVadAYdOqlDZ9AZK1a9QV9wLMs4Lv5bPH6xX51BR74+nx+vFFiK79e8Xwm5y1NUxT+yiuJp\n9BoO3DxQIp5BGsjQZAAwyH0QnZw6YWVhhYWwwNbS1thCMu5b/LFva2mLrZUt9lb2NLRuiL21PQ0s\nG2AhLPgt7jeWnVgGgH87f+b3nl/lweXqsDxiOVfuXOHLEV+WWbGrtWq+PPslmy5twtXOlZcffZmw\n22EsO7mMLi5d+MT3kyqZy1AwH0qLQaHGOJl4kjdC3kCj1/DBoA8Y1WZUmfGy8rMIux3GqnOrymxR\nzPGew1+7/7VWp77uvL6TxaGLzeLBbumxpWy7to0tE7egNWgJiQvhUNwhLqVfAsCjkQfDWg3Dt5Uv\nvdx6VXpK8anEU6w4s4IzyWfo4NSBt/u9XcLTX21StHBveufpLOq/qNT5UFUoS48vRZWtYkSrEdhb\n2xN8IxhHG0de6fkKUzpMURar1SBKV5JCveDP89FffvTlcl0oGqSByNRIVkSs4ETiiVLnB7UcxGu9\nXis1sGtutAYtE7ZPwNXOlY3+VXcBWmTBNdArkLf6lnRVkpiTyOH4wxyKO0R4Qjj5hnwcrB0Y5D4I\n31a+DHEfUu5q8qjUKL448wVht8NoateUed3mMbXT1DqzKHo7+zYzgmcYx2eKOxs6m3yWlWdXcizh\nGADujdxJUidhkAae6PwEL/V46b5ZOX8/oygGhXpDvj6fj058xE9XfzKuYDXVvHRqbipfnf2KrVe3\nljpna2nLG73fYGTrkTXSF73lyhaWHl/Kt2O+pX+L/lXKw1SfD2qtmuMJxwmJDyEkLoS0vDQshSU9\nmvVgqMdQfD188WzsiRCC63eu8+XZL/n11q842TrxXNfneKLzE3Xq9S0rP4tZe2eRrE5mg/8Go82p\ncynnWHl2JWG3w0rEb2jVkKkdpzLDawatHJSFarWFohgU6h07ru3gg+Mf4GDjwBt93mB8u/GV+hLX\n6rX8dPUn/n2ibMuc/Vr0Y3y78fRy60Urh1bVblFo9Br8t/nTpnEb1oxdU+n0Rd0qlfUSZ5AGolKj\nOBR3iMPxh7ly50qpONYW1sztNpenvJ6qc4ui+fp8Xjj4AmeSz7Bq1Cr6tuhLZEokX537ilBVaIm4\nze2bE/hIIFM7Ta1wXYOC+VEUg0K95Er6Fd479h6RqZH0a96PRf0X0a5xu0rnozfoOZtylq/Pfk14\nYniZcUa3GU1vt970cutFB6cOVeq73nBxA8tOLjOuhq6MfI/veZwcbQ5Bk4OqtVI37HYY8w7MKxU+\nrNUwhnoMZaj7UNzs3aqcf3XQGrT88+g/2XtjL/8e8m/aOrZl5dmVHFEdKRHP28Wb2d6zGdVmlOI8\npw5RFINCvUVv0LPt2jY+P/05efo8nvZ5mrld51arK+RG5g1+j/udNVFryNRklhmnf4v++Lj64OPi\ng4+rj0mVqVqrZtz2cXi5ePHfUf81WZ6iweuPh36MXzs/k9MVIaUk7HYYGy5tIFQVio2FDVM7TmW2\n92xuZN7gcPxhDscf5nbObaDAvelQj6EM9RiKj4tPrQzgpuelM//QfE4lncLHxYfbObdJz0svEWdk\n65HM6jKLR5s9+lD7Wq4vKIpBod6TmpvKJ6c+YU/MHjwaebCo/yKzOP9Jz0vnSPwRjiUcK+E/4s80\ntWuKt6u3UVF4u3iX6cJydeRqlkcsZ/P4zSb5Ds7V5TJhxwTcGrqxyX9TpSrEXF0uu6N3s+nSJmIy\nY3C1c2V65+lM6zyt1LhMkZmOkPgQDscf5mzKWQzSgJOtE32a96F/i/70a9GP1g6tzV4pX0i7wPQ9\nZbtO6eLShYD2AYxsPbLaBgcVzIuiGBTuG8ITwvng+AfEZsUyus1o3urzltm6RqSUXM+4zrHbxzie\ncJzQ26FGO1Fl4d7InY5NOpYw9tbUrinjd4ynj1sflo9YXuE1vz3/LSvOrGCd3zp6ufUySc7EnER+\nvPIjP139iUxNJl7OXjzV5Sn82vqZvOo3U5NJqCqU0NuhhCeEk6ROAgr69fs270u/Fv3wcfWhrWPb\nKpsi+SX2F+aHzC8VbmNhw6L+ixjeani1fYEo1ByKYlC4r8jX57M2ai3fnP8GIQQT209kptdMs3tU\n0+q1nEs5x/GE4xxPOE5UalQp+1B/xkpYGVclj2kzBn9Pf9o3bo97I/dSlXZ6Xjr+2/3p27wvK0as\nKF8Wg5bwhHCCrgdx4OYBDBgY2XokM71mVrvrRUrJzaybhCeEE54YzonEE8YuNntre7ycvfB28cbb\n1RvPxp642LnQxLZJiS6ou/l3OZt8lqDoIH6O/bnM67w/8H3Gth1735hXf9hRFIPCfUlcVhzfRX3H\nnpg9aPQaBrQYwMwuMxnsPrhGDO6ptWqiUqM4l3LO6EHsjuaOSWmLLIp6NPIwGpPbcGkDmZpM1o5d\nSy+3XqUqd71Bz+mk0+yL3cfBmwfJ0GTgYO3A1I5TedLryRozFGeQBqIzormQdoELqRe4mHaRy+mX\nS3ivM5W/P/p35njPUewX3YcoikHhvuZO3h22Xt3K5subSc5Npq1jWwK9AgloH1CjX6dSSuLuxhkV\nxbmUc1y9c7VU95OtpS12VnY0sGpAA8sGBWaq/2SjyM7KDvdG7jg3cCbublwpo3bujdyZ8cgMJraf\niJOtU40MzkopycrPKjCKqE4iMSfRuB9/N56I5IgK87CzsuO5rs8xx3uO4gfhPkdRDAoPBFq9ll9u\n/sLGixuJSovCwdqBv3T6C9MfmV5rZpjVWjUX0y5yIvEEX5/7GgAHGwfu5t81xnFp4EJaXhoAXs5e\n2FvbE5kaWabDmrKwsbDB0daxhE2kIiuyJcIK7SjpDXry9HlodBo0Bk3Br15TwgKrRq8hV5drsgwA\nno09GdduHL3detO1aVdsLW0rUVIK9R1FMSg8UEgpOZdyjk2XNnHg5gH0Uk8Hpw70dutNn+Z96N28\nt8mrqavD/534P364/AN7puzBxtKG63eucy3jGusurCM1N7XctF1cuuDRyANbS1usLa2xtrAmT5dH\nnj6PPF0eOoPOaOFVSkm+Ib+Uye0iU9yWFpbYWBR8vRc37CelRK1TG430lYdzA2e8XLzo7dab3m69\n8XbxVrqHHnBqRTEIIaYBSwAvoK+UsszaWgjhBywHLIHVUsqPCsOdgR+BtkAs8LiUssIOXkUxPNwk\n5iQSHBPMyaSTRCRFkKvLBagVRZGYk2gcXJ7QfgJnk88SkRzBtTvXjHGaNWxGS/uWNLdvjqeTJ7na\n3IIunEI/F8nq5AoHvC2FJQ2tGmJnZYedtR3WFtbGlkCRItEatOXmYWNhg7uDe4kxkFYOrYxOdpQB\n44eP2lIMXoABWAW8UZZiEEJYAleB0UA8cBJ4Ukp5UQixDEiXUn4khFgINJFSvvXnPP6MohgUitAa\ntFxKu8SJxBOcSjxFRHJJRdG9aXdc7FyMvggcbRyN5sKL9ov3m2v1WtLy0kjNTS21peUWhJ9NOWuM\nb29tT442B4AJnhP4Z/9/VujfQG/QGz2mqbVq1Dq10adFkV8L475OTa42F61Bi62VLQ0sG9DAqgG2\nlrbG8Y3iv7aWtjS2bYxHIw+aNmxa7zzkKdQttdqVJIQ4xL0VwwBgiZRybOHxPwCklP8WQlwBhkkp\nE4QQLYBDUsrOFV1PUQwK90Jr0HIx7SInE09yKvEUF9IukKnJLNePgp2VHQ42Dmj0mnuumm5s2xjX\nBq642rmiNWiJSI7AuYEz/x31X2b/PJuezXry9aivldW9CvWa+uSoxx2IK3YcDxR5P3GTUhZN1UgE\n6sbgi8IDg7WFNd2bdqd70+481/U5oGCqZrY2m0xNJlmaLDLzC36z8rOMvo+z8rOwsbTB1c611Obc\nwLnUbJwd13bwTtg7PL7ncRysHVgycImiFBQeGCpUDEKIg0BZ69oXSSl3mUsQKaUUQtzzs04I8Tzw\nPEDr1q3NdVmFh4AiV5qONo5gutvicpnScQoavYb0vHSmdpyqmH5QeKCoUDFIKct2u2U6KqC4wXWP\nwjCAJCFEi2JdScnlyPEN8A0UdCVVUyYFhWoz/ZGybQUpKNzv1MbI1EmgoxCinRDCBpgOBBWeCwJm\nF+7PBszWAlFQUFBQqBrVUgxCiClCiHhgABAshNhfGN5SCLEXQEqpA/4G7AcuAVuklBcKs/gIGC2E\nuAaMKjxWUFBQUKhDlAVuCgoKCg8Jps5KUiY5KygoKCiUQFEMCgoKCgolUBSDgoKCgkIJFMWgoKCg\noFACRTEoKCgoKJTgvpyVJIRIAW5WIokrUL5N5LqjvspWX+UCRbaqUF/lAkW2qlIV2dpIKZtWFOm+\nVAyVRQhxypQpWnVBfZWtvsoFimxVob7KBYpsVaUmZVO6khQUFBQUSqAoBgUFBQWFEjwsiuGbuhag\nHOqrbPVVLlBkqwr1VS5QZKsqNSbbQzHGoKCgoKBgOg9Li0FBQUFBwUQeGMUghJgmhLgghDAIIe45\nUi+E8BNCXBFCXC/0M10U7iyEOCCEuFb428RMclWYrxCisxDibLEtSwjxauG5JUIIVbFz/uaQy1TZ\nCuPFCiEiC69/qrLpa0o2IUQrIcTvQoiLhc/+lWLnzFpu93pvip0XQogVhefPCyF6mpq2upggW2Ch\nTJFCiDAhRPdi58p8trUo2zAhRGax5/SOqWlrWK4FxWSKEkLohRDOhedquszWCCGShRBR9zhf8++a\nlPKB2AAvoDNwCOh9jziWQDTgCdgA54AuheeWAQsL9xcC/2cmuSqVb6GMiRTMNwZYQoE/7ZooM5Nk\nA2IB1+rem7llA1oAPQv3HYCrxZ6n2cqtvPemWBx/YB8ggP5AuKlpa0G2gUCTwv1xRbKV92xrUbZh\nwJ6qpK1Juf4UfyLwW22UWWH+Q4GeQNQ9ztf4u/bAtBiklJeklFcqiNYXuC6ljJFS5gObgUmF5yYB\n6wv31wOTzSRaZfMdCURLKSuzgK+qVPeea6rMTMpbSpkgpYwo3L9Lgb8PdzPKUER5701xeb+XBRwH\nnESBV0JT0taobFLKMCnlncLD4xR4UawNqnPvNVlulc37SeAHM127QqSUh4H0cqLU+Lv2wCgGE3EH\n4oodx/NHReImpUwo3E8E3Mx0zcrmO53SL+HLhU3GNebsrqmEbBI4KIQ4LQp8b1c2fU3KBoAQoi3w\nKBBeLNhc5Vbee1NRHFPSVofK5v8sBV+bRdzr2dambAMLn9M+IYR3JdPWpFwIIRoCfsC2YsE1WWam\nUOPvWoU+n+sTQoiDQFle1xdJKc3mFlRKKYUQJk/XKk+uyuQrClyfBgD/KBb8NbCUgpdxKfAJ8Ewt\nyzZYSqkSQjQDDgghLhd+1ZiaviZlQwjRiII/7qtSyqzC4GqV24OIEGI4BYphcLHgCp9tDRMBtJZS\nZheOA+0EOtbi9StiIhAqpSz+BV/XZVbj3FeKQUo5qppZqIBWxY49CsMAkoQQLaSUCYXNsmRzyCWE\nqEy+44AIKWVSsbyN+0KIb4E9psplLtmklKrC32QhxA4KmqyHqUaZmUs2IYQ1BUphk5Rye7G8q1Vu\nf6K896aiONYmpK0OpsiGEKIbsBoYJ6VMKwov59nWimzFFDlSyr1CiJVCCFdT0takXMUo1YKv4TIz\nhRp/1x62rqSTQEchRLvCr/PpQFDhuSBgduH+bMBcLZDK5FuqL7OwUixiClDmTIWakk0IYS+EcCja\nB8YUk6GmysxU2QTwHXBJSvnpn86Zs9zKe2+KyzurcMZIfyCzsCvMlLTVocL8hRCtge3AU1LKq8XC\ny3u2tSVb88LniBCiLwV1UpopaWtSrkJ5GgO+FHv3aqHMTKHm37WaGlmv7Y2CP388oAGSgP2F4S2B\nvcXi+VMweyWagi6oonAX4FfgGnAQcDaTXGXmW4Zc9hT8IRr/Kf0GIBI4X/iQW5ixzCqUjYIZDucK\ntwu1UWaVkG0wBV1F54GzhZt/TZRbWe8N8ALwQuG+AL4qPB9JsZlx93rnzFhWFcm2GrhTrIxOVfRs\na1G2vxVe+xwFA+MDa6PcKpKr8HgOsPlP6WqjzH4AEgAtBXXas7X9rikrnxUUFBQUSvCwdSUpKCgo\nKFSAohgUFBQUFEqgKAYFBQUFhRIoikFBQUFBoQSKYlBQUFBQKIGiGBQUFBQUSqAoBgUFBQWFEiiK\nQUFBQUGhBP8P7CRyYOdNlWMAAAAASUVORK5CYII=\n", "text/plain": [ "A visualization of chaos: 41 triple pendulums with very slightly different initial conditions pic.twitter.com/CTiABFVWHW
— Fermat's Library (@fermatslibrary) March 5, 2017